[
{
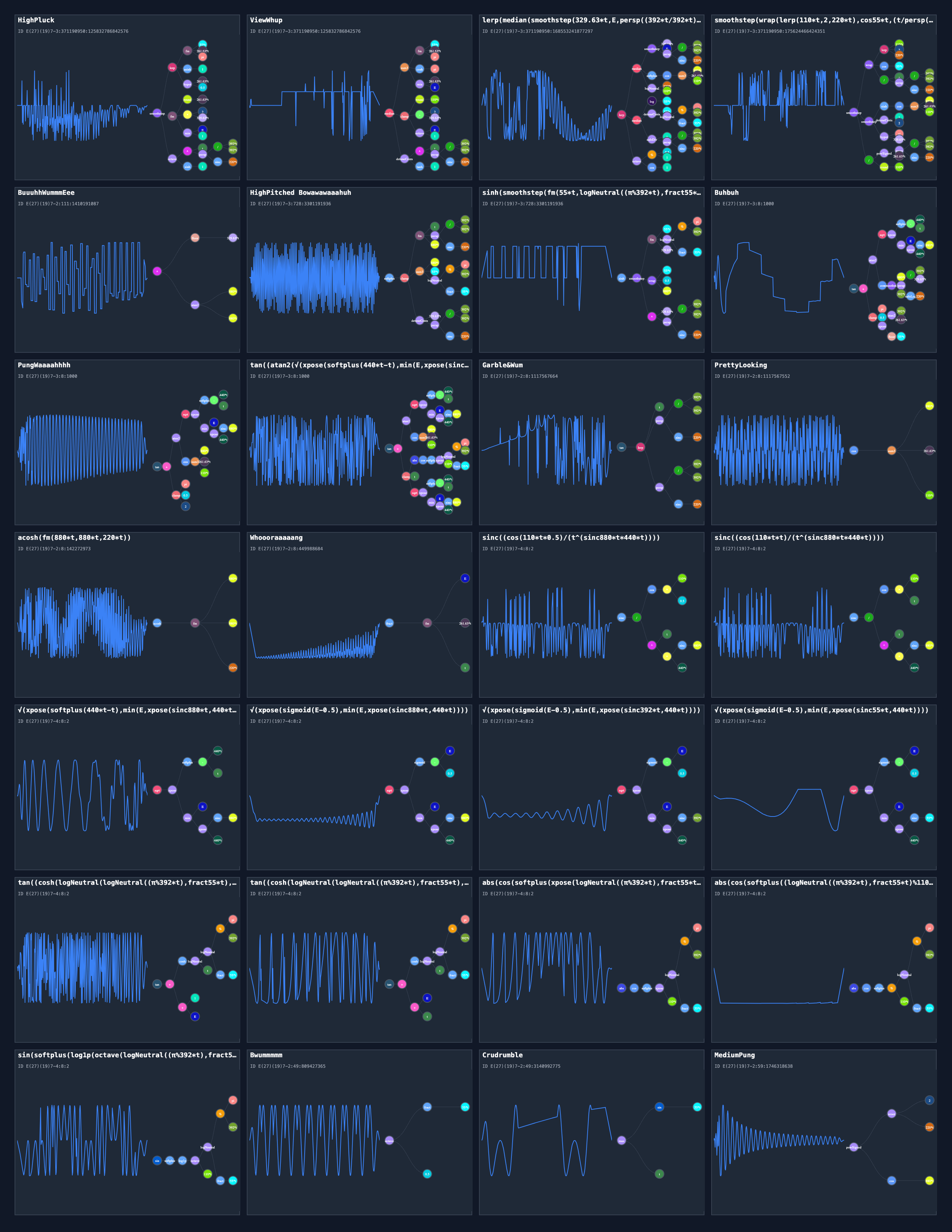
"equation": "smoothstep(lerp(fm(55*t,261.63*t,pi),asinh(1),hypot(261.63*t,0.5)),fm(round(261.63*t),(2 * 329.63*t),min(E,1)),octave((t ^ persp((392*t / 392*t),sinc(220*t))),sinh(1)))",
"fullEquation": "sin(2 * pi * (smoothstep(lerp(fm(55*t,261.63*t,pi),asinh(1),hypot(261.63*t,0.5)),fm(round(261.63*t),(2 * 329.63*t),min(E,1)),octave((t ^ persp((392*t / 392*t),sinc(220*t))),sinh(1)))))",
"friendlyName": "HighPluck",
"id": "E(27)(19)7-3:371190950:125832786842576",
"timestamp": "2025-11-02T18:39:57.163Z",
"depth": 4,
"width": 14,
"leaves": 14,
"nodes": 26,
"leafValues": [
"55*t",
"261.63*t",
"pi",
"1",
"0.5",
"2",
"329.63*t",
"E",
"t",
"persp((392*t / 392*t),sinc(220*t))"
],
"nodeFunctions": [
"asinh",
"round",
"sinh"
]
},
{
"equation": "median(sum3(fm(55*t,261.63*t,pi),cosh(pi),min(261.63*t,E)),clamp(round(110*t),(2 - 329.63*t),octave(E,1)),detuneCents((t ^ persp((392*t / 392*t),sinc(220*t))),tanh(1)))",
"fullEquation": "sin(2 * pi * (median(sum3(fm(55*t,261.63*t,pi),cosh(pi),min(261.63*t,E)),clamp(round(110*t),(2 - 329.63*t),octave(E,1)),detuneCents((t ^ persp((392*t / 392*t),sinc(220*t))),tanh(1)))))",
"friendlyName": "ViewWhup",
"id": "E(27)(19)7-3:371190950:125832786842576",
"timestamp": "2025-11-02T18:39:08.665Z",
"depth": 4,
"width": 14,
"leaves": 14,
"nodes": 26,
"leafValues": [
"55*t",
"261.63*t",
"pi",
"E",
"110*t",
"2",
"329.63*t",
"1",
"t",
"persp((392*t / 392*t),sinc(220*t))"
],
"nodeFunctions": [
"cosh",
"round",
"tanh"
]
},
{
"equation": "lerp(median(smoothstep(329.63*t,E,persp((392*t / 392*t),sinc(220*t))),softplus(cos(sum3(880*t,261.63*t,110*t))),logNeutral(220*t,110*t)),median(log(55*t),detuneCents(55*t,logNeutral((pi % 392*t),fract(55*t))),safeDiv(1,persp((392*t / 392*t),sinc(220*t)))),octave((0.5 % 1),cos(1)))",
"fullEquation": "sin(2 * pi * (lerp(median(smoothstep(329.63*t,E,persp((392*t / 392*t),sinc(220*t))),softplus(cos(sum3(880*t,261.63*t,110*t))),logNeutral(220*t,110*t)),median(log(55*t),detuneCents(55*t,logNeutral((pi % 392*t),fract(55*t))),safeDiv(1,persp((392*t / 392*t),sinc(220*t)))),octave((0.5 % 1),cos(1)))))",
"friendlyName": "",
"id": "E(27)(19)7-3:371190950:168553241877297",
"timestamp": "2025-11-02T18:38:43.239Z",
"depth": 4,
"width": 14,
"leaves": 14,
"nodes": 26,
"leafValues": [
"329.63*t",
"E",
"persp((392*t / 392*t),sinc(220*t))",
"cos(sum3(880*t,261.63*t,110*t))",
"220*t",
"110*t",
"55*t",
"logNeutral((pi % 392*t),fract(55*t))",
"1",
"0.5"
],
"nodeFunctions": [
"softplus",
"log",
"cos"
]
},
{
"equation": "smoothstep(wrap(lerp(110*t,2,220*t),cos(55*t),(t / persp((392*t / 392*t),sinc(220*t)))),smoothstep(sinh(cos(sum3(880*t,261.63*t,110*t))),detuneCents(1,2),hypot(pi,329.63*t)),(powSigned(persp((392*t / 392*t),sinc(220*t)),261.63*t) / round(110*t)))",
"fullEquation": "sin(2 * pi * (smoothstep(wrap(lerp(110*t,2,220*t),cos(55*t),(t / persp((392*t / 392*t),sinc(220*t)))),smoothstep(sinh(cos(sum3(880*t,261.63*t,110*t))),detuneCents(1,2),hypot(pi,329.63*t)),(powSigned(persp((392*t / 392*t),sinc(220*t)),261.63*t) / round(110*t)))))",
"friendlyName": "",
"id": "E(27)(19)7-3:371190950:175624466424351",
"timestamp": "2025-11-02T18:38:00.604Z",
"depth": 4,
"width": 14,
"leaves": 14,
"nodes": 26,
"leafValues": [
"110*t",
"2",
"220*t",
"55*t",
"t",
"persp((392*t / 392*t),sinc(220*t))",
"cos(sum3(880*t,261.63*t,110*t))",
"1",
"pi",
"329.63*t",
"261.63*t"
],
"nodeFunctions": [
"cos",
"sinh",
"round"
]
},
{
"equation": "(floor(329.63*t) ^ atan2(880*t,880*t))",
"fullEquation": "sin(2 * pi * ((floor(329.63*t) ^ atan2(880*t,880*t))))",
"friendlyName": "BuuuhhWummmEee",
"id": "E(27)(19)7-2:111:1410191087",
"timestamp": "2025-11-02T18:34:25.125Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"329.63*t",
"880*t"
],
"nodeFunctions": [
"floor"
]
},
{
"equation": "softplus(clamp(fm(t,persp((392*t / 392*t),sinc(220*t)),880*t),sum3(880*t,55*t,logNeutral((pi % 392*t),fract(55*t))),detuneCents(329.63*t,persp((392*t / 392*t),sinc(220*t)))))",
"fullEquation": "sin(2 * pi * (softplus(clamp(fm(t,persp((392*t / 392*t),sinc(220*t)),880*t),sum3(880*t,55*t,logNeutral((pi % 392*t),fract(55*t))),detuneCents(329.63*t,persp((392*t / 392*t),sinc(220*t)))))))",
"friendlyName": "HighPitched Bowawawaaahuh",
"id": "E(27)(19)7-3:728:3301191936",
"timestamp": "2025-11-02T18:15:03.973Z",
"depth": 4,
"width": 8,
"leaves": 8,
"nodes": 13,
"leafValues": [
"t",
"persp((392*t / 392*t),sinc(220*t))",
"880*t",
"55*t",
"logNeutral((pi % 392*t),fract(55*t))",
"329.63*t"
],
"nodeFunctions": [
"softplus"
]
},
{
"equation": "sinh(smoothstep(fm(55*t,logNeutral((pi % 392*t),fract(55*t)),329.63*t),wrap(55*t,0.5,880*t),(329.63*t ^ persp((392*t / 392*t),sinc(220*t)))))",
"fullEquation": "sin(2 * pi * (sinh(smoothstep(fm(55*t,logNeutral((pi % 392*t),fract(55*t)),329.63*t),wrap(55*t,0.5,880*t),(329.63*t ^ persp((392*t / 392*t),sinc(220*t)))))))",
"friendlyName": "",
"id": "E(27)(19)7-3:728:3301191936",
"timestamp": "2025-11-02T18:14:00.628Z",
"depth": 4,
"width": 8,
"leaves": 8,
"nodes": 13,
"leafValues": [
"55*t",
"logNeutral((pi % 392*t),fract(55*t))",
"329.63*t",
"0.5",
"880*t",
"persp((392*t / 392*t),sinc(220*t))"
],
"nodeFunctions": [
"sinh"
]
},
{
"equation": "tan((atan2(sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t)))),cos(smoothstep(880*t,persp((392*t / 329.63*t),safeLog(220*t)),392*t))) + clamp(pi,0.5,xpose(atan2(392*t,261.63*t),floor(55*t)))))",
"fullEquation": "sin(2 * pi * (tan((atan2(sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t)))),cos(smoothstep(880*t,persp((392*t / 329.63*t),safeLog(220*t)),392*t))) + clamp(pi,0.5,xpose(atan2(392*t,261.63*t),floor(55*t)))))))",
"friendlyName": "Buhbuh",
"id": "E(27)(19)7-3:8:1000",
"timestamp": "2025-11-02T18:11:46.292Z",
"depth": 9,
"width": 8,
"leaves": 15,
"nodes": 34,
"leafValues": [
"pi",
"0.5",
"880*t",
"392*t",
"261.63*t",
"55*t",
"E",
"440*t",
"t",
"329.63*t",
"220*t"
],
"nodeFunctions": [
"tan",
"sqrt",
"cos",
"floor",
"softplus",
"safeLog",
"sinc"
]
},
{
"equation": "tan((atan2(sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t)))),cos(sum3(880*t,261.63*t,110*t))) + clamp(pi,0.5,2)))",
"fullEquation": "sin(2 * pi * (tan((atan2(sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t)))),cos(sum3(880*t,261.63*t,110*t))) + clamp(pi,0.5,2)))))",
"friendlyName": "PungWaaaahhhh",
"id": "E(27)(19)7-3:8:1000",
"timestamp": "2025-11-02T18:09:49.001Z",
"depth": 4,
"width": 5,
"leaves": 5,
"nodes": 9,
"leafValues": [
"sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t))))",
"cos(sum3(880*t,261.63*t,110*t))",
"pi",
"0.5",
"2"
],
"nodeFunctions": [
"tan"
]
},
{
"equation": "tan((atan2(sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t)))),cos(sum3(880*t,261.63*t,110*t))) + clamp(abs(cos(softplus(xpose(logNeutral((pi % 392*t),fract(55*t)),110*t)))),t,sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t)))))))",
"fullEquation": "sin(2 * pi * (tan((atan2(sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t)))),cos(sum3(880*t,261.63*t,110*t))) + clamp(abs(cos(softplus(xpose(logNeutral((pi % 392*t),fract(55*t)),110*t)))),t,sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t)))))))))",
"friendlyName": "",
"id": "E(27)(19)7-3:8:1000",
"timestamp": "2025-11-02T18:09:34.047Z",
"depth": 4,
"width": 5,
"leaves": 5,
"nodes": 9,
"leafValues": [
"sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t))))",
"cos(sum3(880*t,261.63*t,110*t))",
"abs(cos(softplus(xpose(logNeutral((pi % 392*t),fract(55*t)),110*t))))",
"t"
],
"nodeFunctions": [
"tan"
]
},
{
"equation": "tan(lerp(t,persp((392*t / 392*t),sinc(220*t)),persp((392*t / 392*t),sinc(220*t))))",
"fullEquation": "sin(2 * pi * (tan(lerp(t,persp((392*t / 392*t),sinc(220*t)),persp((392*t / 392*t),sinc(220*t))))))",
"friendlyName": "Garble&Wum",
"id": "E(27)(19)7-2:8:1117567664",
"timestamp": "2025-11-02T16:56:49.102Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 5,
"leafValues": [
"t",
"persp((392*t / 392*t),sinc(220*t))"
],
"nodeFunctions": [
"tan"
]
},
{
"equation": "cos(sum3(880*t,261.63*t,110*t))",
"fullEquation": "sin(2 * pi * (cos(sum3(880*t,261.63*t,110*t))))",
"friendlyName": "PrettyLooking",
"id": "E(27)(19)7-2:8:1117567552",
"timestamp": "2025-11-02T16:55:56.973Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 5,
"leafValues": [
"880*t",
"261.63*t",
"110*t"
],
"nodeFunctions": [
"cos"
]
},
{
"equation": "acosh(fm(880*t,880*t,220*t))",
"fullEquation": "sin(2 * pi * (acosh(fm(880*t,880*t,220*t))))",
"friendlyName": "",
"id": "E(27)(19)7-2:8:142272973",
"timestamp": "2025-11-02T16:52:42.694Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 5,
"leafValues": [
"880*t",
"220*t"
],
"nodeFunctions": [
"acosh"
]
},
{
"equation": "fract(fm(E,261.63*t,t))",
"fullEquation": "sin(2 * pi * (fract(fm(E,261.63*t,t))))",
"friendlyName": "Whoooraaaaang",
"id": "E(27)(19)7-2:8:449988684",
"timestamp": "2025-11-02T16:51:11.469Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 5,
"leafValues": [
"E",
"261.63*t",
"t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "sinc((cos((110*t * 0.5)) / (t ^ (sinc(880*t) * 440*t))))",
"fullEquation": "sin(2 * pi * (sinc((cos((110*t * 0.5)) / (t ^ (sinc(880*t) * 440*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:44:41.415Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 12,
"leafValues": [
"t",
"110*t",
"0.5",
"440*t",
"880*t"
],
"nodeFunctions": [
"sinc",
"cos"
]
},
{
"equation": "sinc((cos((110*t * t)) / (t ^ (sinc(880*t) * 440*t))))",
"fullEquation": "sin(2 * pi * (sinc((cos((110*t * t)) / (t ^ (sinc(880*t) * 440*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:44:36.015Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 12,
"leafValues": [
"t",
"110*t",
"440*t",
"880*t"
],
"nodeFunctions": [
"sinc",
"cos"
]
},
{
"equation": "sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t))))",
"fullEquation": "sin(2 * pi * (sqrt(xpose(softplus((440*t - t)),min(E,xpose(sinc(880*t),440*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:43:45.801Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 12,
"leafValues": [
"E",
"440*t",
"t",
"880*t"
],
"nodeFunctions": [
"sqrt",
"softplus",
"sinc"
]
},
{
"equation": "sqrt(xpose(sigmoid((E - 0.5)),min(E,xpose(sinc(880*t),440*t))))",
"fullEquation": "sin(2 * pi * (sqrt(xpose(sigmoid((E - 0.5)),min(E,xpose(sinc(880*t),440*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:43:24.168Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 12,
"leafValues": [
"E",
"0.5",
"440*t",
"880*t"
],
"nodeFunctions": [
"sqrt",
"sigmoid",
"sinc"
]
},
{
"equation": "sqrt(xpose(sigmoid((E - 0.5)),min(E,xpose(sinc(392*t),440*t))))",
"fullEquation": "sin(2 * pi * (sqrt(xpose(sigmoid((E - 0.5)),min(E,xpose(sinc(392*t),440*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:43:18.921Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 12,
"leafValues": [
"E",
"0.5",
"440*t",
"392*t"
],
"nodeFunctions": [
"sqrt",
"sigmoid",
"sinc"
]
},
{
"equation": "sqrt(xpose(sigmoid((E - 0.5)),min(E,xpose(sinc(55*t),440*t))))",
"fullEquation": "sin(2 * pi * (sqrt(xpose(sigmoid((E - 0.5)),min(E,xpose(sinc(55*t),440*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:43:10.002Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 12,
"leafValues": [
"E",
"0.5",
"440*t",
"55*t"
],
"nodeFunctions": [
"sqrt",
"sigmoid",
"sinc"
]
},
{
"equation": "tan((cosh(logNeutral(logNeutral((pi % 392*t),fract(55*t)),t)) + (1 + E)))",
"fullEquation": "sin(2 * pi * (tan((cosh(logNeutral(logNeutral((pi % 392*t),fract(55*t)),t)) + (1 + E)))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:41:14.065Z",
"depth": 5,
"width": 3,
"leaves": 4,
"nodes": 9,
"leafValues": [
"1",
"E",
"logNeutral((pi % 392*t),fract(55*t))",
"t"
],
"nodeFunctions": [
"tan",
"cosh"
]
},
{
"equation": "tan((cosh(logNeutral(logNeutral((pi % 392*t),fract(55*t)),t)) + (E + t)))",
"fullEquation": "sin(2 * pi * (tan((cosh(logNeutral(logNeutral((pi % 392*t),fract(55*t)),t)) + (E + t)))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:40:55.950Z",
"depth": 5,
"width": 3,
"leaves": 4,
"nodes": 9,
"leafValues": [
"E",
"t",
"logNeutral((pi % 392*t),fract(55*t))"
],
"nodeFunctions": [
"tan",
"cosh"
]
},
{
"equation": "abs(cos(softplus(xpose(logNeutral((pi % 392*t),fract(55*t)),110*t))))",
"fullEquation": "sin(2 * pi * (abs(cos(softplus(xpose(logNeutral((pi % 392*t),fract(55*t)),110*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:38:03.089Z",
"depth": 5,
"width": 2,
"leaves": 2,
"nodes": 6,
"leafValues": [
"logNeutral((pi % 392*t),fract(55*t))",
"110*t"
],
"nodeFunctions": [
"abs",
"cos",
"softplus"
]
},
{
"equation": "abs(cos(softplus((logNeutral((pi % 392*t),fract(55*t)) % 110*t))))",
"fullEquation": "sin(2 * pi * (abs(cos(softplus((logNeutral((pi % 392*t),fract(55*t)) % 110*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:37:31.459Z",
"depth": 5,
"width": 2,
"leaves": 2,
"nodes": 6,
"leafValues": [
"logNeutral((pi % 392*t),fract(55*t))",
"110*t"
],
"nodeFunctions": [
"abs",
"cos",
"softplus"
]
},
{
"equation": "sin(softplus(log1p(octave(logNeutral((pi % 392*t),fract(55*t)),110*t))))",
"fullEquation": "sin(2 * pi * (sin(softplus(log1p(octave(logNeutral((pi % 392*t),fract(55*t)),110*t))))))",
"friendlyName": "",
"id": "E(27)(19)7-4:8:2",
"timestamp": "2025-11-02T16:25:34.290Z",
"depth": 5,
"width": 2,
"leaves": 2,
"nodes": 6,
"leafValues": [
"logNeutral((pi % 392*t),fract(55*t))",
"110*t"
],
"nodeFunctions": [
"sin",
"softplus",
"log1p"
]
},
{
"equation": "octave(fract(55*t),0.5)",
"fullEquation": "sin(2 * pi * (octave(fract(55*t),0.5)))",
"friendlyName": "Bwummmmm",
"id": "E(27)(19)7-2:49:809427365",
"timestamp": "2025-11-02T15:52:34.344Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 4,
"leafValues": [
"0.5",
"55*t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "max(sin(55*t),t)",
"fullEquation": "sin(2 * pi * (max(sin(55*t),t)))",
"friendlyName": "Crudrumble",
"id": "E(27)(19)7-2:49:3140992775",
"timestamp": "2025-11-02T15:50:11.006Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 4,
"leafValues": [
"t",
"55*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "powSigned(nroot(2,220*t),cos(880*t))",
"fullEquation": "sin(2 * pi * (powSigned(nroot(2,220*t),cos(880*t))))",
"friendlyName": "MediumPung",
"id": "E(27)(19)7-2:59:1746318638",
"timestamp": "2025-11-02T15:42:13.328Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"2",
"220*t",
"880*t"
],
"nodeFunctions": [
"cos"
]
},
{
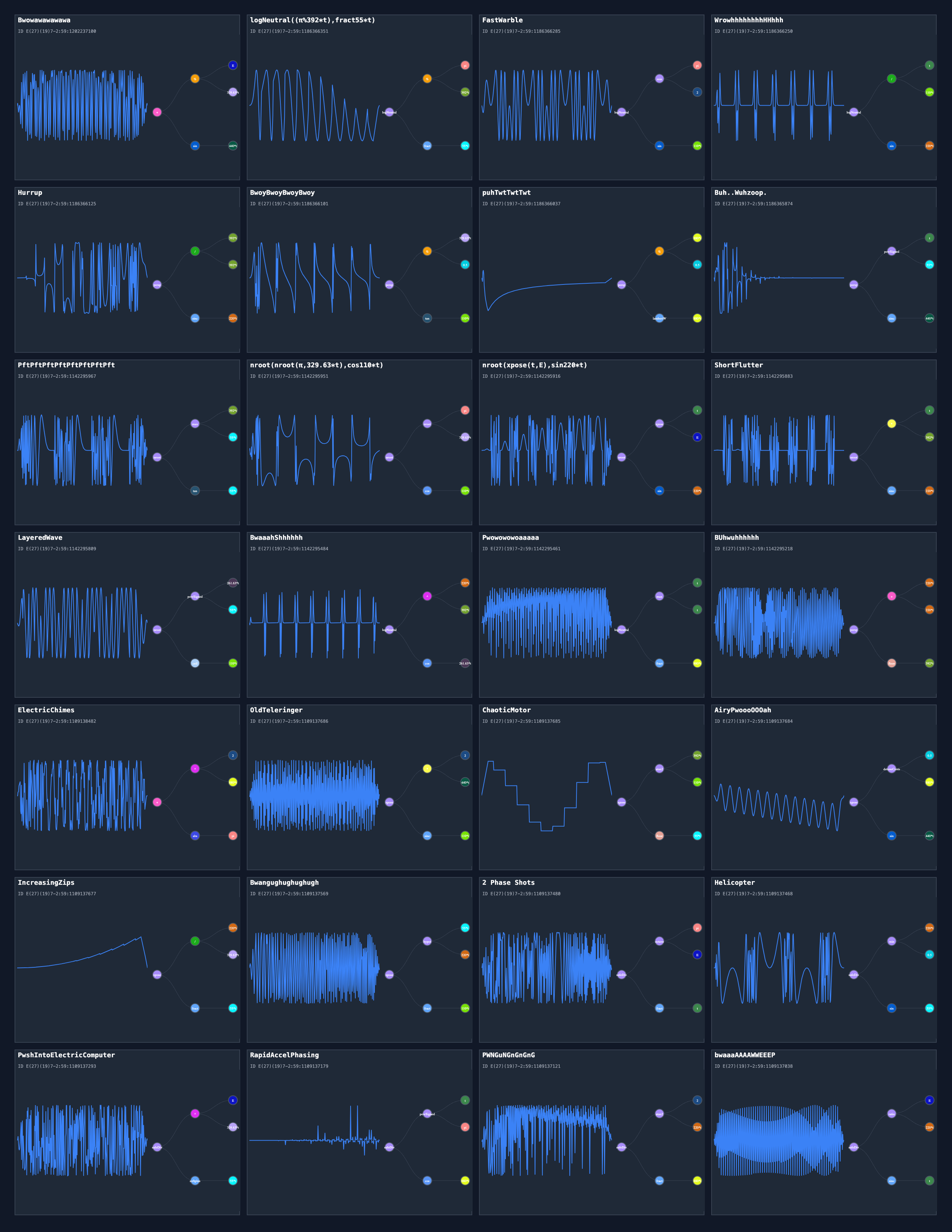
"equation": "((E % 329.63*t) + sin(440*t))",
"fullEquation": "sin(2 * pi * (((E % 329.63*t) + sin(440*t))))",
"friendlyName": "Bwowawawawawa",
"id": "E(27)(19)7-2:59:1202237100",
"timestamp": "2025-11-02T15:41:52.213Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"E",
"329.63*t",
"440*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "logNeutral((pi % 392*t),fract(55*t))",
"fullEquation": "sin(2 * pi * (logNeutral((pi % 392*t),fract(55*t))))",
"friendlyName": "",
"id": "E(27)(19)7-2:59:1186366351",
"timestamp": "2025-11-02T15:40:59.990Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"392*t",
"55*t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "logNeutral(min(pi,2),sin(110*t))",
"fullEquation": "sin(2 * pi * (logNeutral(min(pi,2),sin(110*t))))",
"friendlyName": "FastWarble",
"id": "E(27)(19)7-2:59:1186366285",
"timestamp": "2025-11-02T15:40:33.694Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"2",
"110*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "logNeutral((t / 110*t),sin(220*t))",
"fullEquation": "sin(2 * pi * (logNeutral((t / 110*t),sin(220*t))))",
"friendlyName": "WrowhhhhhhhhHHhhh",
"id": "E(27)(19)7-2:59:1186366250",
"timestamp": "2025-11-02T15:39:56.227Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"110*t",
"220*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "persp((392*t / 392*t),sinc(220*t))",
"fullEquation": "sin(2 * pi * (persp((392*t / 392*t),sinc(220*t))))",
"friendlyName": "Hurrup",
"id": "E(27)(19)7-2:59:1186366125",
"timestamp": "2025-11-02T15:38:46.458Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"392*t",
"220*t"
],
"nodeFunctions": [
"sinc"
]
},
{
"equation": "persp((329.63*t % 0.5),tan(110*t))",
"fullEquation": "sin(2 * pi * (persp((329.63*t % 0.5),tan(110*t))))",
"friendlyName": "BwoyBwoyBwoyBwoy",
"id": "E(27)(19)7-2:59:1186366101",
"timestamp": "2025-11-02T15:38:22.673Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"329.63*t",
"0.5",
"110*t"
],
"nodeFunctions": [
"tan"
]
},
{
"equation": "persp((880*t % 0.5),lambertW(880*t))",
"fullEquation": "sin(2 * pi * (persp((880*t % 0.5),lambertW(880*t))))",
"friendlyName": "puhTwtTwtTwt",
"id": "E(27)(19)7-2:59:1186366037",
"timestamp": "2025-11-02T15:37:45.220Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"880*t",
"0.5"
],
"nodeFunctions": [
"lambertW"
]
},
{
"equation": "persp(powSigned(t,55*t),sinc(440*t))",
"fullEquation": "sin(2 * pi * (persp(powSigned(t,55*t),sinc(440*t))))",
"friendlyName": "Buh..Wuhzoop.",
"id": "E(27)(19)7-2:59:1186365874",
"timestamp": "2025-11-02T15:36:39.272Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"55*t",
"440*t"
],
"nodeFunctions": [
"sinc"
]
},
{
"equation": "nroot(max(392*t,55*t),tan(55*t))",
"fullEquation": "sin(2 * pi * (nroot(max(392*t,55*t),tan(55*t))))",
"friendlyName": "PftPftPftPftPftPftPftPft",
"id": "E(27)(19)7-2:59:1142295967",
"timestamp": "2025-11-02T15:36:08.559Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"392*t",
"55*t"
],
"nodeFunctions": [
"tan"
]
},
{
"equation": "nroot(nroot(pi,329.63*t),cos(110*t))",
"fullEquation": "sin(2 * pi * (nroot(nroot(pi,329.63*t),cos(110*t))))",
"friendlyName": "",
"id": "E(27)(19)7-2:59:1142295951",
"timestamp": "2025-11-02T15:35:56.362Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"329.63*t",
"110*t"
],
"nodeFunctions": [
"cos"
]
},
{
"equation": "nroot(xpose(t,E),sin(220*t))",
"fullEquation": "sin(2 * pi * (nroot(xpose(t,E),sin(220*t))))",
"friendlyName": "",
"id": "E(27)(19)7-2:59:1142295916",
"timestamp": "2025-11-02T15:35:39.106Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"E",
"220*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "nroot((t * 392*t),sinc(220*t))",
"fullEquation": "sin(2 * pi * (nroot((t * 392*t),sinc(220*t))))",
"friendlyName": "ShortFlutter",
"id": "E(27)(19)7-2:59:1142295883",
"timestamp": "2025-11-02T15:35:15.572Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"392*t",
"220*t"
],
"nodeFunctions": [
"sinc"
]
},
{
"equation": "nroot(powSigned(261.63*t,55*t),ceil(110*t))",
"fullEquation": "sin(2 * pi * (nroot(powSigned(261.63*t,55*t),ceil(110*t))))",
"friendlyName": "LayeredWave",
"id": "E(27)(19)7-2:59:1142295809",
"timestamp": "2025-11-02T15:34:34.767Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"261.63*t",
"55*t",
"110*t"
],
"nodeFunctions": [
"ceil"
]
},
{
"equation": "logNeutral((220*t ^ 392*t),cos(261.63*t))",
"fullEquation": "sin(2 * pi * (logNeutral((220*t ^ 392*t),cos(261.63*t))))",
"friendlyName": "BwaaahShhhhhh",
"id": "E(27)(19)7-2:59:1142295484",
"timestamp": "2025-11-02T15:32:36.533Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"220*t",
"392*t",
"261.63*t"
],
"nodeFunctions": [
"cos"
]
},
{
"equation": "logNeutral(max(t,t),fract(880*t))",
"fullEquation": "sin(2 * pi * (logNeutral(max(t,t),fract(880*t))))",
"friendlyName": "Pwowowowoaaaaa",
"id": "E(27)(19)7-2:59:1142295461",
"timestamp": "2025-11-02T15:32:13.325Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"880*t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "persp((220*t + 220*t),floor(392*t))",
"fullEquation": "sin(2 * pi * (persp((220*t + 220*t),floor(392*t))))",
"friendlyName": "BUhwuhhhhhh",
"id": "E(27)(19)7-2:59:1142295218",
"timestamp": "2025-11-02T15:30:58.713Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"220*t",
"392*t"
],
"nodeFunctions": [
"floor"
]
},
{
"equation": "((2 ^ 880*t) + abs(pi))",
"fullEquation": "sin(2 * pi * (((2 ^ 880*t) + abs(pi))))",
"friendlyName": "ElectricChimes",
"id": "E(27)(19)7-2:59:1109138482",
"timestamp": "2025-11-02T15:30:41.389Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"2",
"880*t",
"pi"
],
"nodeFunctions": [
"abs"
]
},
{
"equation": "xpose((2 * 440*t),sinc(110*t))",
"fullEquation": "sin(2 * pi * (xpose((2 * 440*t),sinc(110*t))))",
"friendlyName": "OldTeleringer",
"id": "E(27)(19)7-2:59:1109137686",
"timestamp": "2025-11-02T15:27:04.732Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"2",
"440*t",
"110*t"
],
"nodeFunctions": [
"sinc"
]
},
{
"equation": "xpose(atan2(392*t,110*t),floor(55*t))",
"fullEquation": "sin(2 * pi * (xpose(atan2(392*t,110*t),floor(55*t))))",
"friendlyName": "ChaoticMotor",
"id": "E(27)(19)7-2:59:1109137685",
"timestamp": "2025-11-02T15:26:54.425Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"392*t",
"110*t",
"55*t"
],
"nodeFunctions": [
"floor"
]
},
{
"equation": "xpose(detuneCents(0.5,880*t),sin(440*t))",
"fullEquation": "sin(2 * pi * (xpose(detuneCents(0.5,880*t),sin(440*t))))",
"friendlyName": "AiryPwoooOOOah",
"id": "E(27)(19)7-2:59:1109137684",
"timestamp": "2025-11-02T15:26:38.544Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"0.5",
"880*t",
"440*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "xpose((220*t / 329.63*t),fract(55*t))",
"fullEquation": "sin(2 * pi * (xpose((220*t / 329.63*t),fract(55*t))))",
"friendlyName": "IncreasingZips",
"id": "E(27)(19)7-2:59:1109137677",
"timestamp": "2025-11-02T15:26:10.883Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"220*t",
"329.63*t",
"55*t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "xpose(hypot(55*t,220*t),fract(110*t))",
"fullEquation": "sin(2 * pi * (xpose(hypot(55*t,220*t),fract(110*t))))",
"friendlyName": "Bwangughughughugh",
"id": "E(27)(19)7-2:59:1109137569",
"timestamp": "2025-11-02T15:25:15.838Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"55*t",
"220*t",
"110*t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "safeDiv(octave(pi,E),fract(t))",
"fullEquation": "sin(2 * pi * (safeDiv(octave(pi,E),fract(t))))",
"friendlyName": "2 Phase Shots",
"id": "E(27)(19)7-2:59:1109137480",
"timestamp": "2025-11-02T15:24:32.777Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"E",
"t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "safeDiv(min(220*t,0.5),sin(55*t))",
"fullEquation": "sin(2 * pi * (safeDiv(min(220*t,0.5),sin(55*t))))",
"friendlyName": "Helicopter",
"id": "E(27)(19)7-2:59:1109137468",
"timestamp": "2025-11-02T15:24:10.496Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"220*t",
"0.5",
"55*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "safeDiv((E ^ 329.63*t),softplus(55*t))",
"fullEquation": "sin(2 * pi * (safeDiv((E ^ 329.63*t),softplus(55*t))))",
"friendlyName": "PwshIntoElectricComputer",
"id": "E(27)(19)7-2:59:1109137293",
"timestamp": "2025-11-02T15:23:02.747Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"E",
"329.63*t",
"55*t"
],
"nodeFunctions": [
"softplus"
]
},
{
"equation": "safeDiv(powSigned(t,pi),cos(880*t))",
"fullEquation": "sin(2 * pi * (safeDiv(powSigned(t,pi),cos(880*t))))",
"friendlyName": "RapidAccelPhasing",
"id": "E(27)(19)7-2:59:1109137179",
"timestamp": "2025-11-02T15:21:59.566Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"pi",
"880*t"
],
"nodeFunctions": [
"cos"
]
},
{
"equation": "safeDiv(atan2(2,220*t),fract(880*t))",
"fullEquation": "sin(2 * pi * (safeDiv(atan2(2,220*t),fract(880*t))))",
"friendlyName": "PWNGuNGnGnGnG",
"id": "E(27)(19)7-2:59:1109137121",
"timestamp": "2025-11-02T15:20:15.779Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"2",
"220*t",
"880*t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "safeDiv(ratio(E,220*t),sinc(t))",
"fullEquation": "sin(2 * pi * (safeDiv(ratio(E,220*t),sinc(t))))",
"friendlyName": "bwaaaAAAAWWEEEP",
"id": "E(27)(19)7-2:59:1109137038",
"timestamp": "2025-11-02T15:19:30.013Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"E",
"220*t",
"t"
],
"nodeFunctions": [
"sinc"
]
},
{
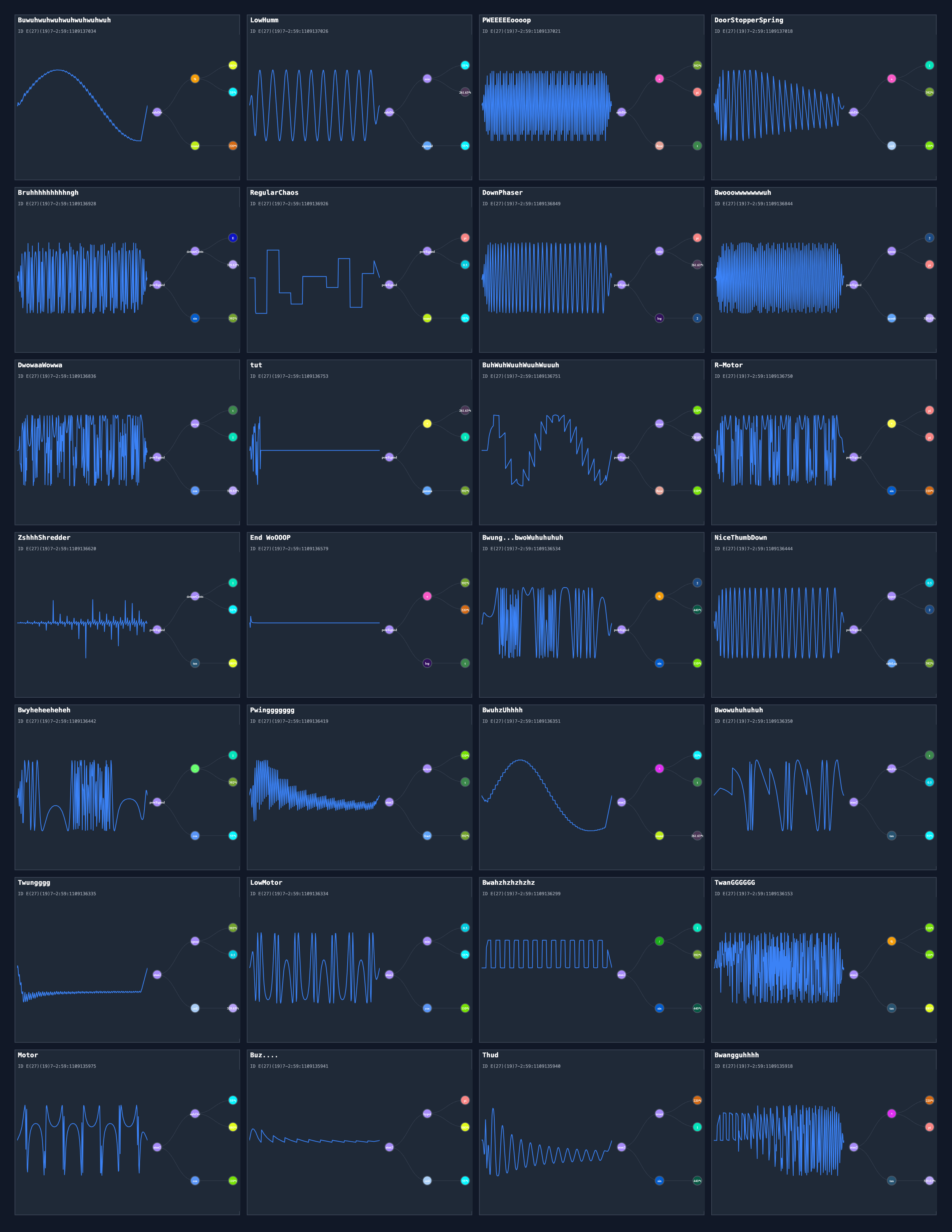
"equation": "safeDiv((880*t % 55*t),round(220*t))",
"fullEquation": "sin(2 * pi * (safeDiv((880*t % 55*t),round(220*t))))",
"friendlyName": "Buwuhwuhwuhwuhwuhwuhwuh",
"id": "E(27)(19)7-2:59:1109137034",
"timestamp": "2025-11-02T15:19:05.701Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"880*t",
"55*t",
"220*t"
],
"nodeFunctions": [
"round"
]
},
{
"equation": "safeDiv(min(55*t,261.63*t),sigmoid(55*t))",
"fullEquation": "sin(2 * pi * (safeDiv(min(55*t,261.63*t),sigmoid(55*t))))",
"friendlyName": "LowHumm",
"id": "E(27)(19)7-2:59:1109137026",
"timestamp": "2025-11-02T15:18:46.096Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"55*t",
"261.63*t"
],
"nodeFunctions": [
"sigmoid"
]
},
{
"equation": "safeDiv((392*t + pi),floor(t))",
"fullEquation": "sin(2 * pi * (safeDiv((392*t + pi),floor(t))))",
"friendlyName": "PWEEEEEoooop",
"id": "E(27)(19)7-2:59:1109137021",
"timestamp": "2025-11-02T15:18:25.723Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"392*t",
"pi",
"t"
],
"nodeFunctions": [
"floor"
]
},
{
"equation": "safeDiv((1 + 392*t),ceil(110*t))",
"fullEquation": "sin(2 * pi * (safeDiv((1 + 392*t),ceil(110*t))))",
"friendlyName": "DoorStopperSpring",
"id": "E(27)(19)7-2:59:1109137018",
"timestamp": "2025-11-02T15:18:12.561Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"1",
"392*t",
"110*t"
],
"nodeFunctions": [
"ceil"
]
},
{
"equation": "powSigned(detuneCents(E,329.63*t),sin(392*t))",
"fullEquation": "sin(2 * pi * (powSigned(detuneCents(E,329.63*t),sin(392*t))))",
"friendlyName": "Bruhhhhhhhhhngh",
"id": "E(27)(19)7-2:59:1109136928",
"timestamp": "2025-11-02T15:17:19.236Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"E",
"329.63*t",
"392*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "powSigned(powSigned(pi,0.5),round(55*t))",
"fullEquation": "sin(2 * pi * (powSigned(powSigned(pi,0.5),round(55*t))))",
"friendlyName": "RegularChaos",
"id": "E(27)(19)7-2:59:1109136926",
"timestamp": "2025-11-02T15:17:05.815Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"0.5",
"55*t"
],
"nodeFunctions": [
"round"
]
},
{
"equation": "powSigned(ratio(pi,261.63*t),log(2))",
"fullEquation": "sin(2 * pi * (powSigned(ratio(pi,261.63*t),log(2))))",
"friendlyName": "DownPhaser",
"id": "E(27)(19)7-2:59:1109136849",
"timestamp": "2025-11-02T15:16:17.344Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"261.63*t",
"2"
],
"nodeFunctions": [
"log"
]
},
{
"equation": "powSigned(xpose(2,pi),acosh(329.63*t))",
"fullEquation": "sin(2 * pi * (powSigned(xpose(2,pi),acosh(329.63*t))))",
"friendlyName": "Bwooowwwwwwwuh",
"id": "E(27)(19)7-2:59:1109136844",
"timestamp": "2025-11-02T15:15:42.048Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"2",
"pi",
"329.63*t"
],
"nodeFunctions": [
"acosh"
]
},
{
"equation": "powSigned(persp(t,1),cos(329.63*t))",
"fullEquation": "sin(2 * pi * (powSigned(persp(t,1),cos(329.63*t))))",
"friendlyName": "DwowaaWowwa",
"id": "E(27)(19)7-2:59:1109136836",
"timestamp": "2025-11-02T15:15:13.672Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"1",
"329.63*t"
],
"nodeFunctions": [
"cos"
]
},
{
"equation": "powSigned((261.63*t * 1),gamma(392*t))",
"fullEquation": "sin(2 * pi * (powSigned((261.63*t * 1),gamma(392*t))))",
"friendlyName": "tut",
"id": "E(27)(19)7-2:59:1109136753",
"timestamp": "2025-11-02T15:14:00.837Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"261.63*t",
"1",
"392*t"
],
"nodeFunctions": [
"gamma"
]
},
{
"equation": "powSigned(nroot(110*t,329.63*t),floor(110*t))",
"fullEquation": "sin(2 * pi * (powSigned(nroot(110*t,329.63*t),floor(110*t))))",
"friendlyName": "BuhWuhWuuhWuuhWuuuh",
"id": "E(27)(19)7-2:59:1109136751",
"timestamp": "2025-11-02T15:13:32.905Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"110*t",
"329.63*t"
],
"nodeFunctions": [
"floor"
]
},
{
"equation": "powSigned((pi * pi),sin(220*t))",
"fullEquation": "sin(2 * pi * (powSigned((pi * pi),sin(220*t))))",
"friendlyName": "R-Motor",
"id": "E(27)(19)7-2:59:1109136750",
"timestamp": "2025-11-02T15:13:20.351Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"220*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "powSigned(detuneCents(1,55*t),tan(880*t))",
"fullEquation": "sin(2 * pi * (powSigned(detuneCents(1,55*t),tan(880*t))))",
"friendlyName": "ZshhhShredder",
"id": "E(27)(19)7-2:59:1109136620",
"timestamp": "2025-11-02T15:12:07.058Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"1",
"55*t",
"880*t"
],
"nodeFunctions": [
"tan"
]
},
{
"equation": "powSigned((392*t + 220*t),log(t))",
"fullEquation": "sin(2 * pi * (powSigned((392*t + 220*t),log(t))))",
"friendlyName": "End WoOOOP",
"id": "E(27)(19)7-2:59:1109136579",
"timestamp": "2025-11-02T15:11:28.191Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"392*t",
"220*t",
"t"
],
"nodeFunctions": [
"log"
]
},
{
"equation": "powSigned((2 % 440*t),sin(110*t))",
"fullEquation": "sin(2 * pi * (powSigned((2 % 440*t),sin(110*t))))",
"friendlyName": "Bwung...bwoWuhuhuhuh",
"id": "E(27)(19)7-2:59:1109136534",
"timestamp": "2025-11-02T15:09:52.211Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"2",
"440*t",
"110*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "powSigned(hypot(0.5,2),safeLog(392*t))",
"fullEquation": "sin(2 * pi * (powSigned(hypot(0.5,2),safeLog(392*t))))",
"friendlyName": "NiceThumbDown",
"id": "E(27)(19)7-2:59:1109136444",
"timestamp": "2025-11-02T15:08:35.161Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"0.5",
"2",
"392*t"
],
"nodeFunctions": [
"safeLog"
]
},
{
"equation": "powSigned((1 - 392*t),cos(55*t))",
"fullEquation": "sin(2 * pi * (powSigned((1 - 392*t),cos(55*t))))",
"friendlyName": "Bwyheheeheheh",
"id": "E(27)(19)7-2:59:1109136442",
"timestamp": "2025-11-02T15:08:07.360Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"1",
"392*t",
"55*t"
],
"nodeFunctions": [
"cos"
]
},
{
"equation": "atan2(octave(110*t,t),fract(392*t))",
"fullEquation": "sin(2 * pi * (atan2(octave(110*t,t),fract(392*t))))",
"friendlyName": "Pwinggggggg",
"id": "E(27)(19)7-2:59:1109136419",
"timestamp": "2025-11-02T15:07:39.695Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"110*t",
"t",
"392*t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "atan2((55*t ^ t),round(261.63*t))",
"fullEquation": "sin(2 * pi * (atan2((55*t ^ t),round(261.63*t))))",
"friendlyName": "BwuhzUhhhh",
"id": "E(27)(19)7-2:59:1109136351",
"timestamp": "2025-11-02T15:06:34.861Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"55*t",
"t",
"261.63*t"
],
"nodeFunctions": [
"round"
]
},
{
"equation": "atan2(safeDiv(t,0.5),tan(55*t))",
"fullEquation": "sin(2 * pi * (atan2(safeDiv(t,0.5),tan(55*t))))",
"friendlyName": "Bwowuhuhuhuh",
"id": "E(27)(19)7-2:59:1109136350",
"timestamp": "2025-11-02T15:06:09.884Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"0.5",
"55*t"
],
"nodeFunctions": [
"tan"
]
},
{
"equation": "atan2(xpose(392*t,0.5),ceil(329.63*t))",
"fullEquation": "sin(2 * pi * (atan2(xpose(392*t,0.5),ceil(329.63*t))))",
"friendlyName": "Twungggg",
"id": "E(27)(19)7-2:59:1109136335",
"timestamp": "2025-11-02T15:05:50.145Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"392*t",
"0.5",
"329.63*t"
],
"nodeFunctions": [
"ceil"
]
},
{
"equation": "atan2(min(0.5,55*t),cos(110*t))",
"fullEquation": "sin(2 * pi * (atan2(min(0.5,55*t),cos(110*t))))",
"friendlyName": "LowMotor",
"id": "E(27)(19)7-2:59:1109136334",
"timestamp": "2025-11-02T15:05:38.200Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"0.5",
"55*t",
"110*t"
],
"nodeFunctions": [
"cos"
]
},
{
"equation": "atan2((1 / 392*t),sin(440*t))",
"fullEquation": "sin(2 * pi * (atan2((1 / 392*t),sin(440*t))))",
"friendlyName": "Bwahzhzhzhzhz",
"id": "E(27)(19)7-2:59:1109136299",
"timestamp": "2025-11-02T15:05:08.771Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"1",
"392*t",
"440*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "atan2((110*t % 110*t),tan(880*t))",
"fullEquation": "sin(2 * pi * (atan2((110*t % 110*t),tan(880*t))))",
"friendlyName": "TwanGGGGGG",
"id": "E(27)(19)7-2:59:1109136153",
"timestamp": "2025-11-02T15:03:41.563Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"110*t",
"880*t"
],
"nodeFunctions": [
"tan"
]
},
{
"equation": "atan2(safeDiv(55*t,880*t),cos(110*t))",
"fullEquation": "sin(2 * pi * (atan2(safeDiv(55*t,880*t),cos(110*t))))",
"friendlyName": "Motor",
"id": "E(27)(19)7-2:59:1109135975",
"timestamp": "2025-11-02T15:02:03.064Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"55*t",
"880*t",
"110*t"
],
"nodeFunctions": [
"cos"
]
},
{
"equation": "atan2(hypot(pi,880*t),ceil(55*t))",
"fullEquation": "sin(2 * pi * (atan2(hypot(pi,880*t),ceil(55*t))))",
"friendlyName": "Buz....",
"id": "E(27)(19)7-2:59:1109135941",
"timestamp": "2025-11-02T15:01:10.387Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"880*t",
"55*t"
],
"nodeFunctions": [
"ceil"
]
},
{
"equation": "atan2(nroot(220*t,1),sin(440*t))",
"fullEquation": "sin(2 * pi * (atan2(nroot(220*t,1),sin(440*t))))",
"friendlyName": "Thud",
"id": "E(27)(19)7-2:59:1109135940",
"timestamp": "2025-11-02T15:00:59.193Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"220*t",
"1",
"440*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "atan2((220*t ^ pi),tan(329.63*t))",
"fullEquation": "sin(2 * pi * (atan2((220*t ^ pi),tan(329.63*t))))",
"friendlyName": "Bwangguhhhh",
"id": "E(27)(19)7-2:59:1109135918",
"timestamp": "2025-11-02T15:00:10.366Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"220*t",
"pi",
"329.63*t"
],
"nodeFunctions": [
"tan"
]
},
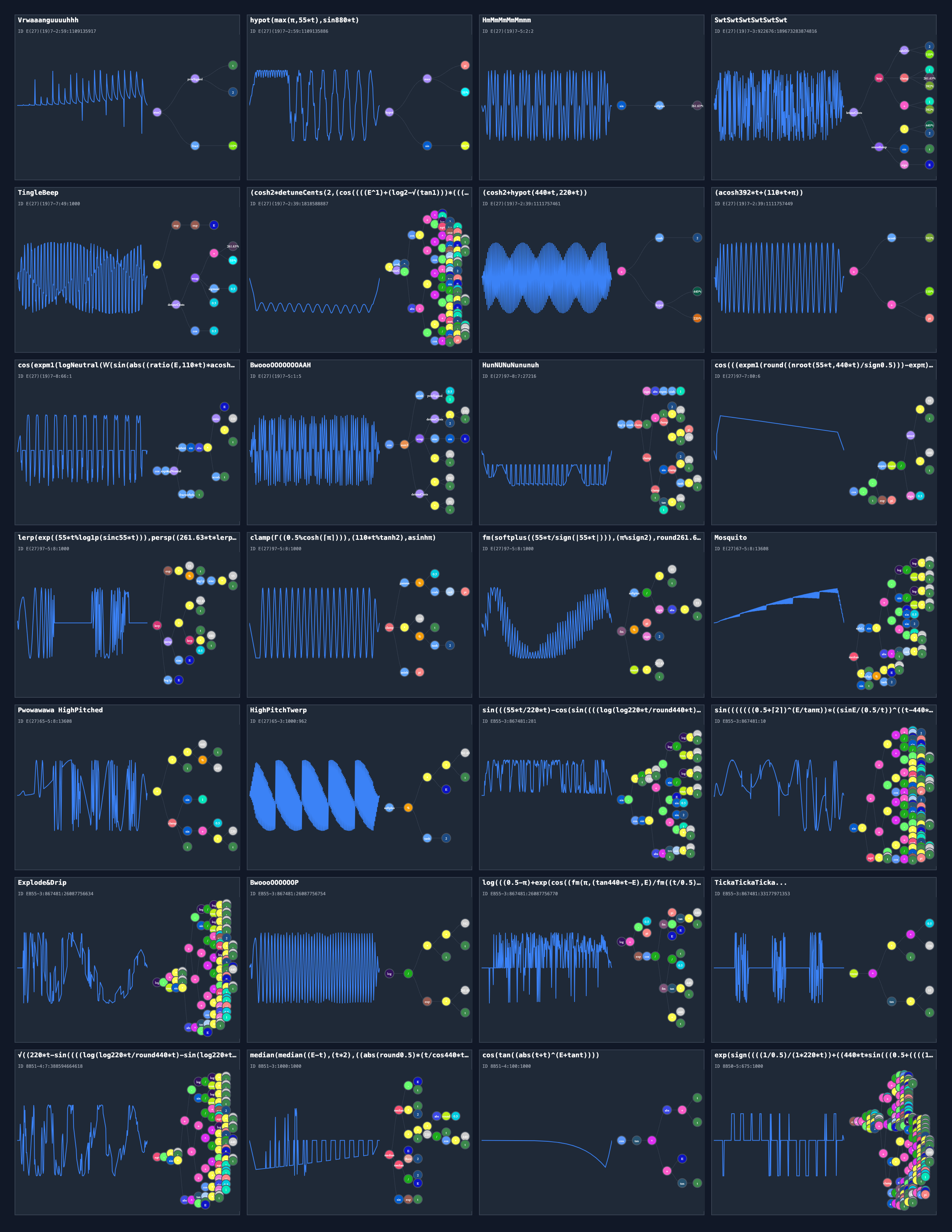
{
"equation": "atan2(powSigned(t,2),fract(110*t))",
"fullEquation": "sin(2 * pi * (atan2(powSigned(t,2),fract(110*t))))",
"friendlyName": "Vrwaaanguuuuhhh",
"id": "E(27)(19)7-2:59:1109135917",
"timestamp": "2025-11-02T15:00:05.908Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"t",
"2",
"110*t"
],
"nodeFunctions": [
"fract"
]
},
{
"equation": "hypot(max(pi,55*t),sin(880*t))",
"fullEquation": "sin(2 * pi * (hypot(max(pi,55*t),sin(880*t))))",
"friendlyName": "",
"id": "E(27)(19)7-2:59:1109135886",
"timestamp": "2025-11-02T14:59:21.456Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"pi",
"55*t",
"880*t"
],
"nodeFunctions": [
"sin"
]
},
{
"equation": "sin(softplus(261.63*t))",
"fullEquation": "sin(2 * pi * (sin(softplus(261.63*t))))",
"friendlyName": "HmMmMmMmMmmm",
"id": "E(27)(19)7-5:2:2",
"timestamp": "2025-11-02T14:57:37.168Z",
"depth": 3,
"width": 1,
"leaves": 1,
"nodes": 3,
"leafValues": [
"261.63*t"
],
"nodeFunctions": [
"sin",
"softplus"
]
},
{
"equation": "detuneCents(lerp(safeDiv(2,110*t),clamp(1,261.63*t,392*t),(1 + 392*t)),smoothstep((440*t * 2),sin(t),sign(E)))",
"fullEquation": "sin(2 * pi * (detuneCents(lerp(safeDiv(2,110*t),clamp(1,261.63*t,392*t),(1 + 392*t)),smoothstep((440*t * 2),sin(t),sign(E)))))",
"friendlyName": "SwtSwtSwtSwtSwtSwt",
"id": "E(27)(19)7-3:922676:189673283874816",
"timestamp": "2025-11-02T14:56:35.188Z",
"depth": 4,
"width": 11,
"leaves": 11,
"nodes": 20,
"leafValues": [
"2",
"110*t",
"1",
"261.63*t",
"392*t",
"440*t",
"t",
"E"
],
"nodeFunctions": [
"sin",
"sign"
]
},
{
"equation": "(exp(exp(E)) * detuneCents(wrap((261.63*t + 55*t),sigmoid(0.5),0.5),cos(0.5)))",
"fullEquation": "sin(2 * pi * ((exp(exp(E)) * detuneCents(wrap((261.63*t + 55*t),sigmoid(0.5),0.5),cos(0.5)))))",
"friendlyName": "TingleBeep",
"id": "E(27)(19)7-7:49:1000",
"timestamp": "2025-11-02T14:46:24.517Z",
"depth": 5,
"width": 5,
"leaves": 6,
"nodes": 14,
"leafValues": [
"E",
"0.5",
"261.63*t",
"55*t"
],
"nodeFunctions": [
"exp",
"cos",
"sigmoid"
]
},
{
"equation": "(cosh(2) * detuneCents(2,(cos((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) - abs(((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))))))",
"fullEquation": "sin(2 * pi * ((cosh(2) * detuneCents(2,(cos((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) - abs(((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))))))))",
"friendlyName": "",
"id": "E(27)(19)7-2:39:1818588887",
"timestamp": "2025-11-02T06:25:48.596Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"2",
"(cos((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) - abs(((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))))"
],
"nodeFunctions": [
"cosh"
]
},
{
"equation": "(cosh(2) + hypot(440*t,220*t))",
"fullEquation": "sin(2 * pi * ((cosh(2) + hypot(440*t,220*t))))",
"friendlyName": "",
"id": "E(27)(19)7-2:39:1111757461",
"timestamp": "2025-11-02T06:24:08.810Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"2",
"440*t",
"220*t"
],
"nodeFunctions": [
"cosh"
]
},
{
"equation": "(acosh(392*t) + (110*t + pi))",
"fullEquation": "sin(2 * pi * ((acosh(392*t) + (110*t + pi))))",
"friendlyName": "",
"id": "E(27)(19)7-2:39:1111757449",
"timestamp": "2025-11-02T06:23:54.032Z",
"depth": 3,
"width": 3,
"leaves": 3,
"nodes": 6,
"leafValues": [
"392*t",
"110*t",
"pi"
],
"nodeFunctions": [
"acosh"
]
},
{
"equation": "cos(expm1(logNeutral(lambertW(sin(abs((ratio(E,110*t) * acosh(t))))),fract(softplus(t)))))",
"fullEquation": "sin(2 * pi * (cos(expm1(logNeutral(lambertW(sin(abs((ratio(E,110*t) * acosh(t))))),fract(softplus(t)))))))",
"friendlyName": "",
"id": "E(27)(19)7-8:66:1",
"timestamp": "2025-11-02T06:21:23.328Z",
"depth": 9,
"width": 3,
"leaves": 4,
"nodes": 15,
"leafValues": [
"t",
"E",
"110*t"
],
"nodeFunctions": [
"cos",
"expm1",
"lambertW",
"fract",
"sin",
"softplus",
"abs",
"acosh"
]
},
{
"equation": "cos(sum3(asinh(powSigned(0.5,1)),wrap(detuneCents(110*t,2),sinc(sin(E)),55*t),detuneCents(392*t,55*t)))",
"fullEquation": "sin(2 * pi * (cos(sum3(asinh(powSigned(0.5,1)),wrap(detuneCents(110*t,2),sinc(sin(E)),55*t),detuneCents(392*t,55*t)))))",
"friendlyName": "BwoooOOOOOOOAAH",
"id": "E(27)(19)7-5:1:5",
"timestamp": "2025-11-02T06:18:16.888Z",
"depth": 6,
"width": 6,
"leaves": 8,
"nodes": 17,
"leafValues": [
"55*t",
"392*t",
"0.5",
"1",
"110*t",
"2",
"E"
],
"nodeFunctions": [
"cos",
"asinh",
"sinc",
"sin"
]
},
{
"equation": "log1p(cosh(clamp(sign(abs(expm1(sinh(1)))),t,clamp((t + clamp(2,110*t,(pi * 110*t))),clamp(sin(clamp(2,55*t,tanh(220*t))),tan(440*t),1),t))))",
"fullEquation": "sin(2 * pi * (log1p(cosh(clamp(sign(abs(expm1(sinh(1)))),t,clamp((t + clamp(2,110*t,(pi * 110*t))),clamp(sin(clamp(2,55*t,tanh(220*t))),tan(440*t),1),t))))))",
"friendlyName": "HunNUNuNununuh",
"id": "E(27)97-8:7:27216",
"timestamp": "2025-11-02T06:13:25.463Z",
"depth": 9,
"width": 6,
"leaves": 13,
"nodes": 29,
"leafValues": [
"t",
"1",
"2",
"110*t",
"440*t",
"pi",
"55*t",
"220*t"
],
"nodeFunctions": [
"log1p",
"cosh",
"sign",
"abs",
"expm1",
"sin",
"tan",
"sinh",
"tanh"
]
},
{
"equation": "cos(((expm1(round((nroot(55*t,440*t) / sign(0.5)))) - exp(pi)) - t))",
"fullEquation": "sin(2 * pi * (cos(((expm1(round((nroot(55*t,440*t) / sign(0.5)))) - exp(pi)) - t))))",
"friendlyName": "",
"id": "E(27)97-7:80:6",
"timestamp": "2025-11-02T06:11:13.137Z",
"depth": 8,
"width": 3,
"leaves": 5,
"nodes": 14,
"leafValues": [
"t",
"pi",
"55*t",
"440*t",
"0.5"
],
"nodeFunctions": [
"cos",
"-",
"expm1",
"exp",
"round",
"sign"
]
},
{
"equation": "lerp(exp((55*t % log1p(sinc(55*t)))),persp((261.63*t * lerp(t,880*t,0.5)),sinc(E)),log1p(E))",
"fullEquation": "sin(2 * pi * (lerp(exp((55*t % log1p(sinc(55*t)))),persp((261.63*t * lerp(t,880*t,0.5)),sinc(E)),log1p(E))))",
"friendlyName": "",
"id": "E(27)97-5:8:1000",
"timestamp": "2025-11-02T06:01:37.101Z",
"depth": 6,
"width": 5,
"leaves": 8,
"nodes": 18,
"leafValues": [
"E",
"55*t",
"261.63*t",
"t",
"880*t",
"0.5"
],
"nodeFunctions": [
"exp",
"persp",
"log1p",
"%",
"*",
"sinc"
]
},
{
"equation": "clamp(gamma((0.5 % cosh(ceil(pi)))),(110*t % tanh(2)),asinh(pi))",
"fullEquation": "sin(2 * pi * (clamp(gamma((0.5 % cosh(ceil(pi)))),(110*t % tanh(2)),asinh(pi))))",
"friendlyName": "",
"id": "E(27)97-5:8:1000",
"timestamp": "2025-11-02T06:00:14.855Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 13,
"leafValues": [
"110*t",
"pi",
"0.5",
"2"
],
"nodeFunctions": [
"gamma",
"%",
"asinh",
"tanh",
"cosh",
"ceil"
]
},
{
"equation": "fm(softplus((55*t / sign(abs(55*t)))),(pi % sign(2)),round(261.63*t))",
"fullEquation": "sin(2 * pi * (fm(softplus((55*t / sign(abs(55*t)))),(pi % sign(2)),round(261.63*t))))",
"friendlyName": "",
"id": "E(27)97-5:8:1000",
"timestamp": "2025-11-02T05:58:55.583Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 13,
"leafValues": [
"pi",
"261.63*t",
"55*t",
"2"
],
"nodeFunctions": [
"softplus",
"%",
"round",
"/",
"sign",
"abs"
]
},
{
"equation": "median(safeLog(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((E - sin(0.5)) - (sin(2) + (1 - 220*t)))) * abs((tan(ceil(440*t)) ^ t))))),(t * softplus(((261.63*t * E) % tanh(2)))),sin(t))",
"fullEquation": "sin(2 * pi * (median(safeLog(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((E - sin(0.5)) - (sin(2) + (1 - 220*t)))) * abs((tan(ceil(440*t)) ^ t))))),(t * softplus(((261.63*t * E) % tanh(2)))),sin(t))))",
"friendlyName": "Mosquito",
"id": "E(27)67-5:8:13608",
"timestamp": "2025-11-02T05:54:35.816Z",
"depth": 3,
"width": 4,
"leaves": 4,
"nodes": 8,
"leafValues": [
"sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((E - sin(0.5)) - (sin(2) + (1 - 220*t)))) * abs((tan(ceil(440*t)) ^ t))))",
"t",
"softplus(((261.63*t * E) % tanh(2)))"
],
"nodeFunctions": [
"safeLog",
"*",
"sin"
]
},
{
"equation": "((440*t % 440*t) * clamp(sin(1),sin((0.5 + 220*t)),t))",
"fullEquation": "sin(2 * pi * (((440*t % 440*t) * clamp(sin(1),sin((0.5 + 220*t)),t))))",
"friendlyName": "Pwowawawa HighPitched",
"id": "E(27)65-5:8:13608",
"timestamp": "2025-11-02T05:51:11.758Z",
"depth": 5,
"width": 5,
"leaves": 6,
"nodes": 12,
"leafValues": [
"440*t",
"t",
"1",
"0.5",
"220*t"
],
"nodeFunctions": [
"*",
"%",
"sin",
"+"
]
},
{
"equation": "softplus(((261.63*t * E) % tanh(2)))",
"fullEquation": "sin(2 * pi * (softplus(((261.63*t * E) % tanh(2)))))",
"friendlyName": "HighPitchTwerp",
"id": "E(27)65-3:1000:962",
"timestamp": "2025-11-02T05:48:05.809Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"261.63*t",
"E",
"2"
],
"nodeFunctions": [
"softplus",
"%",
"*",
"tanh"
]
},
{
"equation": "sin(((55*t / 220*t) - cos(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((E - sin(0.5)) - (sin(2) + (1 - 220*t)))) * abs((tan(ceil(440*t)) ^ t)))))))",
"fullEquation": "sin(2 * pi * (sin(((55*t / 220*t) - cos(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((E - sin(0.5)) - (sin(2) + (1 - 220*t)))) * abs((tan(ceil(440*t)) ^ t)))))))))",
"friendlyName": "",
"id": "EB55-3:867481:281",
"timestamp": "2025-11-02T05:33:40.605Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"55*t",
"220*t",
"sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((E - sin(0.5)) - (sin(2) + (1 - 220*t)))) * abs((tan(ceil(440*t)) ^ t))))"
],
"nodeFunctions": [
"sin",
"-",
"/",
"cos"
]
},
{
"equation": "sin(((((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t)))) + ((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))) * sqrt(220*t)))",
"fullEquation": "sin(2 * pi * (sin(((((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t)))) + ((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))) * sqrt(220*t)))))",
"friendlyName": "",
"id": "EB55-3:867481:10",
"timestamp": "2025-11-02T05:32:41.292Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))",
"220*t"
],
"nodeFunctions": [
"sin",
"*",
"+",
"sqrt"
]
},
{
"equation": "log(((55*t + 55*t) - round(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E))))))))",
"fullEquation": "sin(2 * pi * (log(((55*t + 55*t) - round(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E))))))))))",
"friendlyName": "Explode&Drip",
"id": "EB55-3:867481:26087756634",
"timestamp": "2025-11-02T05:29:59.594Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"55*t",
"sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))"
],
"nodeFunctions": [
"log",
"-",
"+",
"round"
]
},
{
"equation": "log(((392*t * t) / exp(261.63*t)))",
"fullEquation": "sin(2 * pi * (log(((392*t * t) / exp(261.63*t)))))",
"friendlyName": "BwoooOOOOOOP",
"id": "EB55-3:867481:26087756754",
"timestamp": "2025-11-02T05:29:10.424Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"392*t",
"t",
"261.63*t"
],
"nodeFunctions": [
"log",
"/",
"*",
"exp"
]
},
{
"equation": "log(((0.5 - pi) + exp(cos((fm(pi,(tan(440*t) - E),E) / fm((t / 0.5),tan(440*t),440*t))))))",
"fullEquation": "sin(2 * pi * (log(((0.5 - pi) + exp(cos((fm(pi,(tan(440*t) - E),E) / fm((t / 0.5),tan(440*t),440*t))))))))",
"friendlyName": "",
"id": "EB55-3:867481:26087756770",
"timestamp": "2025-11-02T05:28:55.485Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"0.5",
"pi",
"cos((fm(pi,(tan(440*t) - E),E) / fm((t / 0.5),tan(440*t),440*t)))"
],
"nodeFunctions": [
"log",
"+",
"-",
"exp"
]
},
{
"equation": "round(((0.5 ^ 220*t) ^ tan(55*t)))",
"fullEquation": "sin(2 * pi * (round(((0.5 ^ 220*t) ^ tan(55*t)))))",
"friendlyName": "TickaTickaTicka...",
"id": "EB55-3:867481:33177971353",
"timestamp": "2025-11-02T05:27:59.747Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"0.5",
"220*t",
"55*t"
],
"nodeFunctions": [
"round",
"^",
"tan"
]
},
{
"equation": "sqrt((220*t - sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))))",
"fullEquation": "sin(2 * pi * (sqrt((220*t - sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))))))",
"friendlyName": "",
"id": "8B51-4:7:388594664618",
"timestamp": "2025-11-02T05:22:04.792Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 4,
"leafValues": [
"220*t",
"sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))"
],
"nodeFunctions": [
"sqrt",
"-"
]
},
{
"equation": "median(median((E - t),(t * 2),((abs(round(0.5)) * (t / cos(440*t))) * 220*t)),median(E,floor(2),(2 / E)),sin(exp(t)))",
"fullEquation": "sin(2 * pi * (median(median((E - t),(t * 2),((abs(round(0.5)) * (t / cos(440*t))) * 220*t)),median(E,floor(2),(2 / E)),sin(exp(t)))))",
"friendlyName": "",
"id": "8B51-3:1000:1000",
"timestamp": "2025-11-02T05:14:39.963Z",
"depth": 4,
"width": 10,
"leaves": 11,
"nodes": 21,
"leafValues": [
"E",
"t",
"2",
"(abs(round(0.5)) * (t / cos(440*t)))",
"220*t"
],
"nodeFunctions": [
"sin",
"-",
"*",
"floor",
"/",
"exp"
]
},
{
"equation": "cos(tan((abs((t + t)) ^ (E + tan(t)))))",
"fullEquation": "sin(2 * pi * (cos(tan((abs((t + t)) ^ (E + tan(t)))))))",
"friendlyName": "",
"id": "8B51-4:100:1000",
"timestamp": "2025-11-02T05:11:00.965Z",
"depth": 6,
"width": 3,
"leaves": 4,
"nodes": 11,
"leafValues": [
"E",
"t"
],
"nodeFunctions": [
"cos",
"tan",
"^",
"abs",
"+"
]
},
{
"equation": "exp(sign((((1 / 0.5) / (1 * 220*t)) + ((440*t * sin(((0.5 + ((((1 - cos(E)) / (220*t + round(440*t))) + ((tan(E) - (pi ^ 1)) * ((t ^ t) + (t * pi)))) + ((((pi * t) + sign(0.5)) ^ ((E / 0.5) - abs(1))) / sign((sqrt(E) ^ exp(220*t)))))) + ((tan(ceil(220*t)) ^ (440*t - E)) + clamp(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) * ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E))))),cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((exp(((0.5 + E) + cos(pi))) / 440*t),sqrt(t),pi))),sin((tan(ceil(440*t)) ^ (t + t)))))))) - round(2)))))",
"fullEquation": "sin(2 * pi * (exp(sign((((1 / 0.5) / (1 * 220*t)) + ((440*t * sin(((0.5 + ((((1 - cos(E)) / (220*t + round(440*t))) + ((tan(E) - (pi ^ 1)) * ((t ^ t) + (t * pi)))) + ((((pi * t) + sign(0.5)) ^ ((E / 0.5) - abs(1))) / sign((sqrt(E) ^ exp(220*t)))))) + ((tan(ceil(220*t)) ^ (440*t - E)) + clamp(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) * ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E))))),cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((exp(((0.5 + E) + cos(pi))) / 440*t),sqrt(t),pi))),sin((tan(ceil(440*t)) ^ (t + t)))))))) - round(2)))))))",
"friendlyName": "",
"id": "8B50-5:675:1000",
"timestamp": "2025-11-02T00:50:58.600Z",
"depth": 6,
"width": 7,
"leaves": 7,
"nodes": 16,
"leafValues": [
"1",
"0.5",
"220*t",
"440*t",
"sin(((0.5 + ((((1 - cos(E)) / (220*t + round(440*t))) + ((tan(E) - (pi ^ 1)) * ((t ^ t) + (t * pi)))) + ((((pi * t) + sign(0.5)) ^ ((E / 0.5) - abs(1))) / sign((sqrt(E) ^ exp(220*t)))))) + ((tan(ceil(220*t)) ^ (440*t - E)) + clamp(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) * ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E))))),cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((exp(((0.5 + E) + cos(pi))) / 440*t),sqrt(t),pi))),sin((tan(ceil(440*t)) ^ (t + t)))))))",
"2"
],
"nodeFunctions": [
"exp",
"sign",
"+",
"/",
"-",
"*",
"round"
]
},
{
"equation": "sin(((0.5 + ((((1 - cos(E)) / (220*t + round(440*t))) + ((tan(E) - (pi ^ 1)) * ((t ^ t) + (t * pi)))) + ((((pi * t) + sign(0.5)) ^ ((E / 0.5) - abs(1))) / sign((sqrt(E) ^ exp(220*t)))))) + ((tan(ceil(220*t)) ^ (440*t - E)) + clamp(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) * ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E))))),cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((exp(((0.5 + E) + cos(pi))) / 440*t),sqrt(t),pi))),sin((tan(ceil(440*t)) ^ (t + t)))))))",
"fullEquation": "sin(2 * pi * (sin(((0.5 + ((((1 - cos(E)) / (220*t + round(440*t))) + ((tan(E) - (pi ^ 1)) * ((t ^ t) + (t * pi)))) + ((((pi * t) + sign(0.5)) ^ ((E / 0.5) - abs(1))) / sign((sqrt(E) ^ exp(220*t)))))) + ((tan(ceil(220*t)) ^ (440*t - E)) + clamp(sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) * ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E))))),cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((exp(((0.5 + E) + cos(pi))) / 440*t),sqrt(t),pi))),sin((tan(ceil(440*t)) ^ (t + t)))))))))",
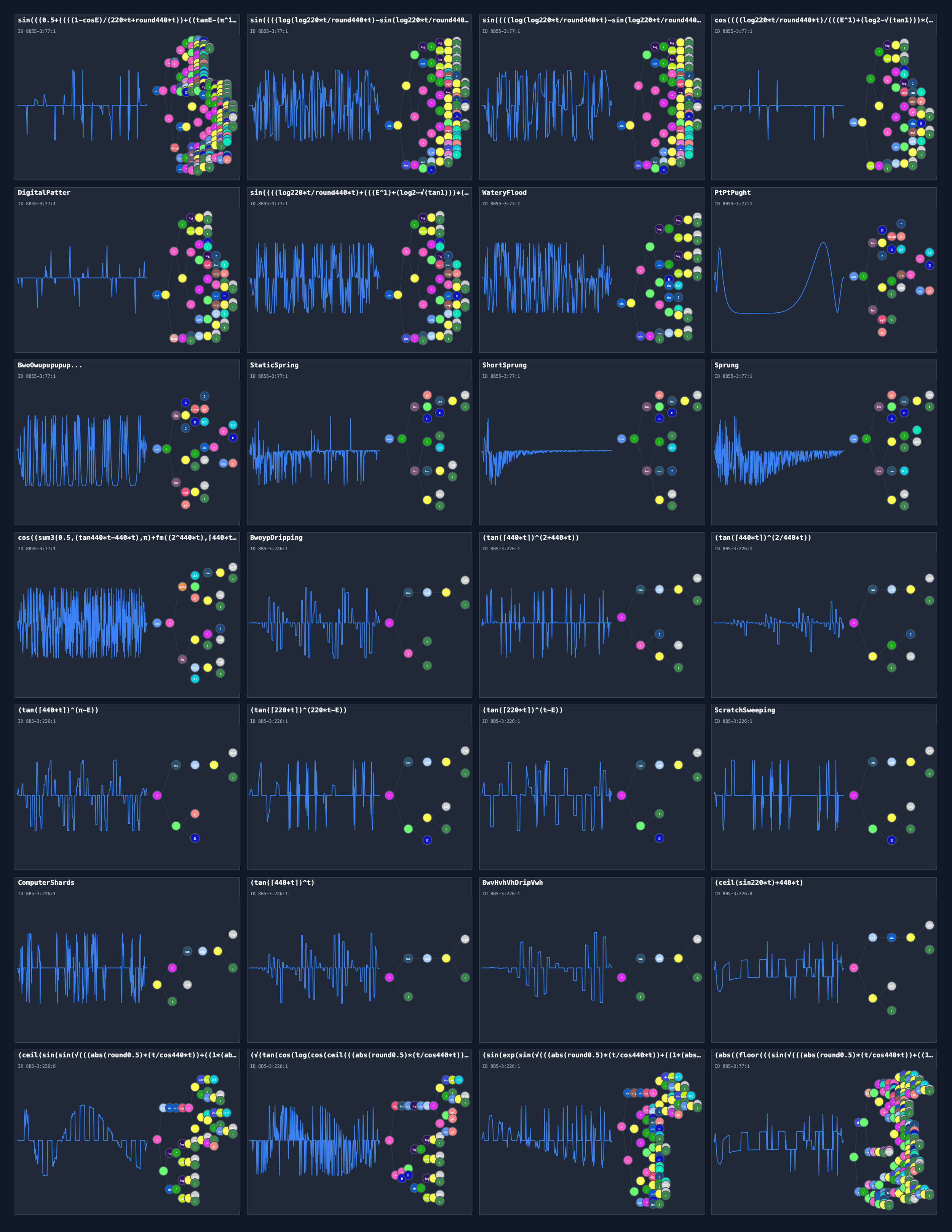
"friendlyName": "sin(((0.5+((((1-cosE)/(220*t+round440*t))+((tanE-(π^1))*((t^t)+(t*π))))+((((π*t)+sign0.5)^((E/0.5)-|1|))/sign(√E^exp220*t))))+((tan(⌈220*t⌉)^(440*t-E))+clamp(sin((((log(log220*t/round440*t)-sin(log220*t/round440*t))*((((0.5+exp2)/(1/√440*t))+((log220*t^(π*2))^((E/440*t)/(π*E))))+((((E-220*t)^√1)+((0.5*1)*signπ))+cos(|0.5|*sign1))))*abs((tan(⌈220*t⌉)^(t-E))))),cos((fm(E,(clamp(2,π,0.5)*E),2)/fm((exp(((0.5+E)+cosπ))/440*t),√t,π))),sin((tan(⌈440*t⌉)^(t+t)))))))",
"id": "8B55-3:77:1",
"timestamp": "2025-11-02T00:04:15.995Z",
"depth": 6,
"width": 4,
"leaves": 6,
"nodes": 12,
"leafValues": [
"0.5",
"((((1 - cos(E)) / (220*t + round(440*t))) + ((tan(E) - (pi ^ 1)) * ((t ^ t) + (t * pi)))) + ((((pi * t) + sign(0.5)) ^ ((E / 0.5) - abs(1))) / sign((sqrt(E) ^ exp(220*t)))))",
"(tan(ceil(220*t)) ^ (440*t - E))",
"sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) * ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))",
"cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((exp(((0.5 + E) + cos(pi))) / 440*t),sqrt(t),pi)))",
"(tan(ceil(440*t)) ^ (t + t))"
],
"nodeFunctions": [
"sin",
"+"
]
},
{
"equation": "sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) * ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))",
"fullEquation": "sin(2 * pi * (sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) * ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))))",
"friendlyName": "sin((((log(log220*t/round440*t)-sin(log220*t/round440*t))*((((0.5+exp2)/(1/√440*t))+((log220*t^(π*2))^((E/440*t)/(π*E))))+((((E-220*t)^√1)+((0.5*1)*signπ))+cos(|0.5|*sign1))))*abs((tan(⌈220*t⌉)^(t-E)))))",
"id": "8B55-3:77:1",
"timestamp": "2025-11-02T00:01:21.907Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"(log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t))))",
"((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))",
"(tan(ceil(220*t)) ^ (t - E))"
],
"nodeFunctions": [
"sin",
"*",
"abs"
]
},
{
"equation": "sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))",
"fullEquation": "sin(2 * pi * (sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))) * abs((tan(ceil(220*t)) ^ (t - E)))))))",
"friendlyName": "",
"id": "8B55-3:77:1",
"timestamp": "2025-11-02T00:00:27.415Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"(log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t))))",
"((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))",
"(tan(ceil(220*t)) ^ (t - E))"
],
"nodeFunctions": [
"sin",
"*",
"+",
"abs"
]
},
{
"equation": "cos((((log(220*t) / round(440*t)) / (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) * round((tan(ceil(220*t)) ^ t))))",
"fullEquation": "sin(2 * pi * (cos((((log(220*t) / round(440*t)) / (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) * round((tan(ceil(220*t)) ^ t))))))",
"friendlyName": "",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:59:59.361Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"(log(220*t) / round(440*t))",
"(((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))",
"(tan(ceil(220*t)) ^ t)"
],
"nodeFunctions": [
"cos",
"*",
"/",
"round"
]
},
{
"equation": "sin((((log(220*t) / round(440*t)) + (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) * floor((tan(ceil(440*t)) ^ t))))",
"fullEquation": "sin(2 * pi * (sin((((log(220*t) / round(440*t)) + (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) * floor((tan(ceil(440*t)) ^ t))))))",
"friendlyName": "DigitalPatter",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:59:27.471Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"(log(220*t) / round(440*t))",
"(((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))",
"(tan(ceil(440*t)) ^ t)"
],
"nodeFunctions": [
"sin",
"*",
"+",
"floor"
]
},
{
"equation": "sin((((log(220*t) / round(440*t)) + (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) * abs((tan(ceil(440*t)) ^ t))))",
"fullEquation": "sin(2 * pi * (sin((((log(220*t) / round(440*t)) + (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) * abs((tan(ceil(440*t)) ^ t))))))",
"friendlyName": "",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:59:19.498Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"(log(220*t) / round(440*t))",
"(((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))",
"(tan(ceil(440*t)) ^ t)"
],
"nodeFunctions": [
"sin",
"*",
"+",
"abs"
]
},
{
"equation": "sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((E - sin(0.5)) - (sin(2) + (1 - 220*t)))) * abs((tan(ceil(440*t)) ^ t))))",
"fullEquation": "sin(2 * pi * (sin((((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + ((E - sin(0.5)) - (sin(2) + (1 - 220*t)))) * abs((tan(ceil(440*t)) ^ t))))))",
"friendlyName": "WateryFlood",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:59:02.569Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"(log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t))))",
"((E - sin(0.5)) - (sin(2) + (1 - 220*t)))",
"(tan(ceil(440*t)) ^ t)"
],
"nodeFunctions": [
"sin",
"*",
"+",
"abs"
]
},
{
"equation": "cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((exp(((0.5 + E) + cos(pi))) / 440*t),sqrt(t),pi)))",
"fullEquation": "sin(2 * pi * (cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((exp(((0.5 + E) + cos(pi))) / 440*t),sqrt(t),pi)))))",
"friendlyName": "PtPtPught",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:57:16.958Z",
"depth": 8,
"width": 6,
"leaves": 12,
"nodes": 24,
"leafValues": [
"E",
"2",
"pi",
"440*t",
"t",
"0.5"
],
"nodeFunctions": [
"cos",
"/",
"*",
"sqrt",
"exp",
"+"
]
},
{
"equation": "cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((sin(((0.5 + E) + cos(pi))) / 220*t),sqrt(220*t),pi)))",
"fullEquation": "sin(2 * pi * (cos((fm(E,(clamp(2,pi,0.5) * E),2) / fm((sin(((0.5 + E) + cos(pi))) / 220*t),sqrt(220*t),pi)))))",
"friendlyName": "BwoOwupupupup...",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:56:35.394Z",
"depth": 8,
"width": 6,
"leaves": 12,
"nodes": 24,
"leafValues": [
"E",
"2",
"pi",
"220*t",
"0.5"
],
"nodeFunctions": [
"cos",
"/",
"*",
"sqrt",
"sin",
"+"
]
},
{
"equation": "cos((fm(pi,(tan(440*t) - E),E) / fm((t / 0.5),tan(440*t),440*t)))",
"fullEquation": "sin(2 * pi * (cos((fm(pi,(tan(440*t) - E),E) / fm((t / 0.5),tan(440*t),440*t)))))",
"friendlyName": "StaticSpring",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:55:08.561Z",
"depth": 6,
"width": 6,
"leaves": 8,
"nodes": 16,
"leafValues": [
"pi",
"E",
"440*t",
"t",
"0.5"
],
"nodeFunctions": [
"cos",
"/",
"-",
"tan"
]
},
{
"equation": "cos((fm(pi,(tan(440*t) - E),E) / fm((t / 0.5),tan(2),440*t)))",
"fullEquation": "sin(2 * pi * (cos((fm(pi,(tan(440*t) - E),E) / fm((t / 0.5),tan(2),440*t)))))",
"friendlyName": "ShortSprung",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:54:57.829Z",
"depth": 6,
"width": 6,
"leaves": 8,
"nodes": 16,
"leafValues": [
"pi",
"E",
"440*t",
"t",
"0.5",
"2"
],
"nodeFunctions": [
"cos",
"/",
"-",
"tan"
]
},
{
"equation": "cos((fm(pi,(tan(440*t) - E),E) / fm((1 / 440*t),tan(0.5),440*t)))",
"fullEquation": "sin(2 * pi * (cos((fm(pi,(tan(440*t) - E),E) / fm((1 / 440*t),tan(0.5),440*t)))))",
"friendlyName": "Sprung",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:54:39.828Z",
"depth": 6,
"width": 6,
"leaves": 8,
"nodes": 16,
"leafValues": [
"pi",
"E",
"440*t",
"1",
"0.5"
],
"nodeFunctions": [
"cos",
"/",
"-",
"tan"
]
},
{
"equation": "cos((sum3(0.5,(tan(440*t) - 440*t),pi) + fm((2 ^ 440*t),ceil(440*t),0.5)))",
"fullEquation": "sin(2 * pi * (cos((sum3(0.5,(tan(440*t) - 440*t),pi) + fm((2 ^ 440*t),ceil(440*t),0.5)))))",
"friendlyName": "",
"id": "8B55-3:77:1",
"timestamp": "2025-11-01T23:54:19.188Z",
"depth": 6,
"width": 6,
"leaves": 8,
"nodes": 16,
"leafValues": [
"0.5",
"pi",
"440*t",
"2"
],
"nodeFunctions": [
"cos",
"+",
"-",
"^",
"ceil",
"tan"
]
},
{
"equation": "(tan(ceil(440*t)) ^ (t + t))",
"fullEquation": "sin(2 * pi * ((tan(ceil(440*t)) ^ (t + t))))",
"friendlyName": "BwoypDripping",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:52:20.126Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"t",
"440*t"
],
"nodeFunctions": [
"^",
"tan",
"+",
"ceil"
]
},
{
"equation": "(tan(ceil(440*t)) ^ (2 + 440*t))",
"fullEquation": "sin(2 * pi * ((tan(ceil(440*t)) ^ (2 + 440*t))))",
"friendlyName": "",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:52:09.347Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"2",
"440*t"
],
"nodeFunctions": [
"^",
"tan",
"+",
"ceil"
]
},
{
"equation": "(tan(ceil(440*t)) ^ (2 / 440*t))",
"fullEquation": "sin(2 * pi * ((tan(ceil(440*t)) ^ (2 / 440*t))))",
"friendlyName": "",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:52:03.943Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"2",
"440*t"
],
"nodeFunctions": [
"^",
"tan",
"/",
"ceil"
]
},
{
"equation": "(tan(ceil(440*t)) ^ (pi - E))",
"fullEquation": "sin(2 * pi * ((tan(ceil(440*t)) ^ (pi - E))))",
"friendlyName": "",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:51:47.283Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"pi",
"E",
"440*t"
],
"nodeFunctions": [
"^",
"tan",
"-",
"ceil"
]
},
{
"equation": "(tan(ceil(220*t)) ^ (220*t - E))",
"fullEquation": "sin(2 * pi * ((tan(ceil(220*t)) ^ (220*t - E))))",
"friendlyName": "(tan(⌈220*t⌉)^(220*t-E))",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:51:20.434Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"220*t",
"E"
],
"nodeFunctions": [
"^",
"tan",
"-",
"ceil"
]
},
{
"equation": "(tan(ceil(220*t)) ^ (t - E))",
"fullEquation": "sin(2 * pi * ((tan(ceil(220*t)) ^ (t - E))))",
"friendlyName": "",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:50:58.793Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"t",
"E",
"220*t"
],
"nodeFunctions": [
"^",
"tan",
"-",
"ceil"
]
},
{
"equation": "(tan(ceil(220*t)) ^ (440*t - E))",
"fullEquation": "sin(2 * pi * ((tan(ceil(220*t)) ^ (440*t - E))))",
"friendlyName": "ScratchSweeping",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:50:19.461Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 7,
"leafValues": [
"440*t",
"E",
"220*t"
],
"nodeFunctions": [
"^",
"tan",
"-",
"ceil"
]
},
{
"equation": "(tan(ceil(220*t)) ^ 220*t)",
"fullEquation": "sin(2 * pi * ((tan(ceil(220*t)) ^ 220*t)))",
"friendlyName": "ComputerShards",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:49:28.068Z",
"depth": 4,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"220*t"
],
"nodeFunctions": [
"^",
"tan",
"ceil"
]
},
{
"equation": "(tan(ceil(440*t)) ^ t)",
"fullEquation": "sin(2 * pi * ((tan(ceil(440*t)) ^ t)))",
"friendlyName": "",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:48:46.692Z",
"depth": 4,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"t",
"440*t"
],
"nodeFunctions": [
"^",
"tan",
"ceil"
]
},
{
"equation": "(tan(ceil(220*t)) ^ t)",
"fullEquation": "sin(2 * pi * ((tan(ceil(220*t)) ^ t)))",
"friendlyName": "BwvHvhVhDripVwh",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:48:04.751Z",
"depth": 4,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"t",
"220*t"
],
"nodeFunctions": [
"^",
"tan",
"ceil"
]
},
{
"equation": "(ceil(sin(220*t)) + 440*t)",
"fullEquation": "sin(2 * pi * ((abs((floor(((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) ^ 1) - (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t)))))) - cos(sign((((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t)))) ^ 220*t))))) - cos((sign(cos((ceil((abs(round(0.5)) * (t / cos(440*t)))) - cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))))) / ((E - sin(0.5)) - (sin(2) + (1 - 220*t))))))))",
"friendlyName": "",
"id": "8B5-3:226:8",
"timestamp": "2025-11-01T23:45:43.687Z",
"depth": 4,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"440*t",
"220*t"
],
"nodeFunctions": [
"+",
"ceil",
"sin"
]
},
{
"equation": "(ceil(sin(sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))))) + (log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))))",
"fullEquation": "sin(2 * pi * ((ceil(sin(sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))))) + (log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))))))",
"friendlyName": "",
"id": "8B5-3:226:8",
"timestamp": "2025-11-01T23:44:50.223Z",
"depth": 4,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"(log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t))))",
"sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))"
],
"nodeFunctions": [
"+",
"ceil",
"sin"
]
},
{
"equation": "(sqrt(tan(cos(log(cos(ceil(((abs(round(0.5)) * (t / cos(440*t))) ^ ((pi - pi) + cos(pi))))))))) + (((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + E) + E))",
"fullEquation": "sin(2 * pi * ((sqrt(tan(cos(log(cos(ceil(((abs(round(0.5)) * (t / cos(440*t))) ^ ((pi - pi) + cos(pi))))))))) + (((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t)))) + E) + E))))",
"friendlyName": "",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:41:50.897Z",
"depth": 4,
"width": 3,
"leaves": 4,
"nodes": 9,
"leafValues": [
"E",
"cos(log(cos(ceil(((abs(round(0.5)) * (t / cos(440*t))) ^ ((pi - pi) + cos(pi)))))))",
"(log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t))))"
],
"nodeFunctions": [
"+",
"sqrt",
"tan"
]
},
{
"equation": "(sin(exp(sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))))) + ((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((E ^ tan(t))))))",
"fullEquation": "sin(2 * pi * ((sin(exp(sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))))) + ((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((E ^ tan(t))))))))",
"friendlyName": "",
"id": "8B5-3:226:1",
"timestamp": "2025-11-01T23:40:50.813Z",
"depth": 4,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((E ^ tan(t)))))",
"sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))"
],
"nodeFunctions": [
"+",
"sin",
"exp"
]
},
{
"equation": "(abs((floor(((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) ^ 1) - (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t)))))) - cos(sign((((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t)))) ^ 220*t))))) - cos((sign(cos((ceil((abs(round(0.5)) * (t / cos(440*t)))) - cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))))) / ((E - sin(0.5)) - (sin(2) + (1 - 220*t))))))",
"fullEquation": "sin(2 * pi * ((abs((floor(((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) ^ 1) - (((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t)))))) - cos(sign((((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t)))) ^ 220*t))))) - cos((sign(cos((ceil((abs(round(0.5)) * (t / cos(440*t)))) - cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))))) / ((E - sin(0.5)) - (sin(2) + (1 - 220*t))))))))",
"friendlyName": "",
"id": "8B5-3:77:1",
"timestamp": "2025-11-01T23:38:22.225Z",
"depth": 8,
"width": 6,
"leaves": 8,
"nodes": 23,
"leafValues": [
"((E - sin(0.5)) - (sin(2) + (1 - 220*t)))",
"(((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))",
"sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))",
"1",
"((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))",
"220*t",
"cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))",
"(abs(round(0.5)) * (t / cos(440*t)))"
],
"nodeFunctions": [
"-",
"abs",
"cos",
"/",
"floor",
"sign",
"^",
"ceil"
]
},
{
"equation": "(tan((sin(((220*t ^ 0.5) + 0.5)) - exp(sqrt((E + 2))))) - ceil((sqrt(round((sqrt(220*t) * t))) * pi)))",
"fullEquation": "sin(2 * pi * ((tan((sin(((220*t ^ 0.5) + 0.5)) - exp(sqrt((E + 2))))) - ceil((sqrt(round((sqrt(220*t) * t))) * pi)))))",
"friendlyName": "",
"id": "8B5-3:77:1",
"timestamp": "2025-11-01T23:38:15.509Z",
"depth": 8,
"width": 6,
"leaves": 8,
"nodes": 23,
"leafValues": [
"pi",
"0.5",
"220*t",
"E",
"2",
"t"
],
"nodeFunctions": [
"-",
"tan",
"ceil",
"*",
"sin",
"exp",
"sqrt",
"+",
"round",
"^"
]
},
{
"equation": "(sqrt(tan(sin(sqrt(sign(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))))))))))) + sqrt(((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t)))) * cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))",
"fullEquation": "sin(2 * pi * ((sqrt(tan(sin(sqrt(sign(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))))))))))) + sqrt(((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t)))) * cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))",
"friendlyName": "GarbageCrumple",
"id": "8B5-3:230:1",
"timestamp": "2025-11-01T23:32:44.995Z",
"depth": 4,
"width": 3,
"leaves": 3,
"nodes": 8,
"leafValues": [
"sin(sqrt(sign(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))",
"(((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))",
"cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))"
],
"nodeFunctions": [
"+",
"sqrt",
"tan",
"*"
]
},
{
"equation": "(220*t + ceil(sin(sqrt(log(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))))",
"fullEquation": "sin(2 * pi * ((220*t + ceil(sin(sqrt(log(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))))))",
"friendlyName": "",
"id": "8B5-3:77:1",
"timestamp": "2025-11-01T23:30:14.234Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 4,
"leafValues": [
"220*t",
"sin(sqrt(log(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))"
],
"nodeFunctions": [
"+",
"ceil"
]
},
{
"equation": "(cos((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) / cos(((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))))",
"fullEquation": "sin(2 * pi * ((cos((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) / cos(((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))))))",
"friendlyName": "",
"id": "8B5-3:77:81642589",
"timestamp": "2025-11-01T23:26:32.953Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"(((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))",
"((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))"
],
"nodeFunctions": [
"/",
"cos"
]
},
{
"equation": "(cos((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) - abs(((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))))",
"fullEquation": "sin(2 * pi * ((cos((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))) - abs(((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))))))",
"friendlyName": "",
"id": "8B5-3:77:81642589",
"timestamp": "2025-11-01T23:25:32.556Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"(((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))",
"((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))"
],
"nodeFunctions": [
"-",
"cos",
"abs"
]
},
{
"equation": "(cos(440*t) - abs(t))",
"fullEquation": "sin(2 * pi * ((cos(440*t) - abs(t))))",
"friendlyName": "OohwaOohwaOowhaOohwa",
"id": "8B5-3:77:81642589",
"timestamp": "2025-11-01T23:24:23.954Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"440*t",
"t"
],
"nodeFunctions": [
"-",
"cos",
"abs"
]
},
{
"equation": "((E - sin(0.5)) - (sin(2) + (1 - 220*t)))",
"fullEquation": "sin(2 * pi * (((E - sin(0.5)) - (sin(2) + (1 - 220*t)))))",
"friendlyName": "Pwuuuuuunggggg",
"id": "8B5-3:317:85184000",
"timestamp": "2025-11-01T23:17:47.405Z",
"depth": 4,
"width": 4,
"leaves": 5,
"nodes": 11,
"leafValues": [
"E",
"0.5",
"2",
"1",
"220*t"
],
"nodeFunctions": [
"-",
"+",
"sin"
]
},
{
"equation": "(((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))",
"fullEquation": "sin(2 * pi * ((((E ^ 1) + (log(2) - sqrt(tan(1)))) * (((exp(pi) ^ (t + 440*t)) ^ (sin(E) - exp(440*t))) + cos((ceil(1) - 220*t))))))",
"friendlyName": "Bwuuuuuuuump",
"id": "8B5-5:16506118010:16491622400000",
"timestamp": "2025-11-01T23:17:09.843Z",
"depth": 6,
"width": 8,
"leaves": 11,
"nodes": 29,
"leafValues": [
"E",
"1",
"2",
"220*t",
"pi",
"t",
"440*t"
],
"nodeFunctions": [
"*",
"+",
"^",
"-",
"cos",
"log",
"sqrt",
"tan",
"exp",
"sin",
"ceil"
]
},
{
"equation": "sin(sqrt((440*t + ((E * 220*t) * (2 ^ pi)))))",
"fullEquation": "sin(2 * pi * (sin(sqrt((440*t + ((E * 220*t) * (2 ^ pi)))))))",
"friendlyName": "Deep Wuh",
"id": "8B5-5:77:1",
"timestamp": "2025-11-01T23:00:37.808Z",
"depth": 6,
"width": 4,
"leaves": 5,
"nodes": 11,
"leafValues": [
"440*t",
"E",
"220*t",
"2",
"pi"
],
"nodeFunctions": [
"sin",
"sqrt",
"+",
"*",
"^"
]
},
{
"equation": "((((220*t / exp(1)) + (1 + sin(220*t))) - ((sqrt(1) * (220*t * 0.5)) * ((t + 0.5) * (2 ^ 2)))) ^ ((((440*t * E) / sign(E)) - ((2 * 220*t) / floor(1))) / cos((round(1) * sign(0.5)))))",
"fullEquation": "sin(2 * pi * (((((220*t / exp(1)) + (1 + sin(220*t))) - ((sqrt(1) * (220*t * 0.5)) * ((t + 0.5) * (2 ^ 2)))) ^ ((((440*t * E) / sign(E)) - ((2 * 220*t) / floor(1))) / cos((round(1) * sign(0.5)))))))",
"friendlyName": "LightClick",
"id": "8B5-5:97242270707:11906447336300",
"timestamp": "2025-11-01T22:59:09.397Z",
"depth": 6,
"width": 17,
"leaves": 19,
"nodes": 45,
"leafValues": [
"220*t",
"1",
"0.5",
"t",
"2",
"440*t",
"E"
],
"nodeFunctions": [
"^",
"-",
"/",
"+",
"*",
"cos",
"exp",
"sin",
"sqrt",
"sign",
"floor",
"round"
]
},
{
"equation": "((((440*t * cos(1)) / (2 / log(2))) - ((sin(t) + (0.5 + t)) ^ ((1 / 0.5) ^ (pi ^ 440*t)))) ^ ((((t / 2) ^ exp(E)) - ((1 ^ 440*t) / floor(1))) - tan((log(t) + floor(220*t)))))",
"fullEquation": "sin(2 * pi * (((((440*t * cos(1)) / (2 / log(2))) - ((sin(t) + (0.5 + t)) ^ ((1 / 0.5) ^ (pi ^ 440*t)))) ^ ((((t / 2) ^ exp(E)) - ((1 ^ 440*t) / floor(1))) - tan((log(t) + floor(220*t)))))))",
"friendlyName": "Bwvvvtp",
"id": "8B5-5:97242270707:11906447336267",
"timestamp": "2025-11-01T22:58:42.431Z",
"depth": 6,
"width": 17,
"leaves": 19,
"nodes": 45,
"leafValues": [
"440*t",
"2",
"1",
"t",
"0.5",
"pi",
"E",
"220*t"
],
"nodeFunctions": [
"^",
"-",
"/",
"tan",
"*",
"+",
"cos",
"log",
"sin",
"exp",
"floor"
]
},
{
"equation": "((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))",
"fullEquation": "sin(2 * pi * (((((0.5 + exp(2)) / (1 / sqrt(440*t))) + ((log(220*t) ^ (pi * 2)) ^ ((E / 440*t) / (pi * E)))) + ((((E - 220*t) ^ sqrt(1)) + ((0.5 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))))",
"friendlyName": "BumWooWoooo",
"id": "8B5-5:97242270707:4667293375846",
"timestamp": "2025-11-01T22:57:56.445Z",
"depth": 6,
"width": 17,
"leaves": 19,
"nodes": 45,
"leafValues": [
"0.5",
"1",
"2",
"440*t",
"220*t",
"pi",
"E"
],
"nodeFunctions": [
"+",
"/",
"^",
"cos",
"*",
"exp",
"sqrt",
"log",
"-",
"sign",
"abs"
]
},
{
"equation": "((((0.5 + exp(pi)) / (1 * sqrt(2))) ^ ((exp(440*t) / (t + 1)) * ((t / t) / (pi - E)))) + ((((E + 220*t) ^ sqrt(E)) + ((1 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))",
"fullEquation": "sin(2 * pi * (((((0.5 + exp(pi)) / (1 * sqrt(2))) ^ ((exp(440*t) / (t + 1)) * ((t / t) / (pi - E)))) + ((((E + 220*t) ^ sqrt(E)) + ((1 * 1) * sign(pi))) + cos((abs(0.5) * sign(1)))))))",
"friendlyName": "ShortTut",
"id": "8B5-5:97242270707:4667293375846",
"timestamp": "2025-11-01T22:53:29.616Z",
"depth": 6,
"width": 17,
"leaves": 19,
"nodes": 45,
"leafValues": [
"0.5",
"1",
"pi",
"2",
"440*t",
"t",
"E",
"220*t"
],
"nodeFunctions": [
"+",
"^",
"/",
"*",
"cos",
"exp",
"sqrt",
"-",
"sign",
"abs"
]
},
{
"equation": "((((220*t / tan(2)) - (pi - tan(E))) * ((floor(0.5) + (0.5 * 1)) * ((0.5 ^ 0.5) ^ (0.5 * pi)))) + ((((440*t - 220*t) * sign(220*t)) * ((220*t * 1) - cos(440*t))) - log((sin(220*t) / sin(2)))))",
"fullEquation": "sin(2 * pi * (((((220*t / tan(2)) - (pi - tan(E))) * ((floor(0.5) + (0.5 * 1)) * ((0.5 ^ 0.5) ^ (0.5 * pi)))) + ((((440*t - 220*t) * sign(220*t)) * ((220*t * 1) - cos(440*t))) - log((sin(220*t) / sin(2)))))))",
"friendlyName": "IncreasingPlft",
"id": "8B5-5:97242270707:4667293375845",
"timestamp": "2025-11-01T22:53:20.947Z",
"depth": 6,
"width": 17,
"leaves": 19,
"nodes": 45,
"leafValues": [
"220*t",
"pi",
"2",
"E",
"0.5",
"1",
"440*t"
],
"nodeFunctions": [
"+",
"*",
"-",
"log",
"/",
"^",
"tan",
"floor",
"sign",
"cos",
"sin"
]
},
{
"equation": "((((1 - cos(E)) / (220*t + round(440*t))) + ((tan(E) - (pi ^ 1)) * ((t ^ t) + (t * pi)))) + ((((pi * t) + sign(0.5)) ^ ((E / 0.5) - abs(1))) / sign((sqrt(E) ^ exp(220*t)))))",
"fullEquation": "sin(2 * pi * (((((1 - cos(E)) / (220*t + round(440*t))) + ((tan(E) - (pi ^ 1)) * ((t ^ t) + (t * pi)))) + ((((pi * t) + sign(0.5)) ^ ((E / 0.5) - abs(1))) / sign((sqrt(E) ^ exp(220*t)))))))",
"friendlyName": "PftWaAAEEEE",
"id": "8B5-5:97242270707:4667293375844",
"timestamp": "2025-11-01T22:53:13.673Z",
"depth": 6,
"width": 17,
"leaves": 19,
"nodes": 45,
"leafValues": [
"1",
"220*t",
"E",
"440*t",
"pi",
"t",
"0.5"
],
"nodeFunctions": [
"+",
"/",
"*",
"^",
"sign",
"-",
"cos",
"round",
"tan",
"abs",
"sqrt",
"exp"
]
},
{
"equation": "((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))",
"fullEquation": "sin(2 * pi * (((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((exp(pi) ^ t))))))",
"friendlyName": "ChuwuwuwuwWaaAAwww",
"id": "8B5-5:97242270706:4",
"timestamp": "2025-11-01T22:52:05.739Z",
"depth": 6,
"width": 16,
"leaves": 19,
"nodes": 44,
"leafValues": [
"0.5",
"E",
"t",
"2",
"pi",
"440*t",
"1",
"220*t"
],
"nodeFunctions": [
"+",
"*",
"-",
"^",
"cos",
"/",
"ceil",
"tan",
"sin",
"sqrt",
"exp"
]
},
{
"equation": "((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((E ^ tan(t)))))",
"fullEquation": "sin(2 * pi * (((((0.5 + ceil(2)) ^ (E / tan(pi))) * ((sin(E) / (0.5 / t)) ^ ((t - 440*t) - (2 * E)))) + ((((1 * 1) + sqrt(2)) * ((1 / 220*t) / sin(220*t))) - cos((E ^ tan(t)))))))",
"friendlyName": "DropRepeat2Flood",
"id": "8B5-5:97242270703:4",
"timestamp": "2025-11-01T22:51:51.486Z",
"depth": 6,
"width": 16,
"leaves": 19,
"nodes": 44,
"leafValues": [
"0.5",
"E",
"2",
"pi",
"t",
"440*t",
"1",
"220*t"
],
"nodeFunctions": [
"+",
"*",
"-",
"^",
"cos",
"/",
"ceil",
"tan",
"sin",
"sqrt"
]
},
{
"equation": "((((0.5 ^ 1) + ((440*t ^ 2) - (440*t + 2))) * ((sin(t) - E) * (pi + round(1)))) + (((log(0.5) + 0.5) + sqrt(0.5)) + cos((1 / exp(t)))))",
"fullEquation": "sin(2 * pi * (((((0.5 ^ 1) + ((440*t ^ 2) - (440*t + 2))) * ((sin(t) - E) * (pi + round(1)))) + (((log(0.5) + 0.5) + sqrt(0.5)) + cos((1 / exp(t)))))))",
"friendlyName": "ChewWreeee",
"id": "8B5-5:93793163811:1",
"timestamp": "2025-11-01T22:51:31.210Z",
"depth": 6,
"width": 13,
"leaves": 15,
"nodes": 35,
"leafValues": [
"0.5",
"1",
"E",
"pi",
"440*t",
"2",
"t"
],
"nodeFunctions": [
"+",
"*",
"cos",
"^",
"-",
"sqrt",
"/",
"sin",
"round",
"log",
"exp"
]
},
{
"equation": "((round(abs(pi)) - sin(ceil(1))) + ((cos(440*t) ^ t) - t))",
"fullEquation": "sin(2 * pi * (((round(abs(pi)) - sin(ceil(1))) + ((cos(440*t) ^ t) - t))))",
"friendlyName": "Bwaowawawa",
"id": "8B5-4:139633:6",
"timestamp": "2025-11-01T22:50:44.446Z",
"depth": 5,
"width": 4,
"leaves": 5,
"nodes": 14,
"leafValues": [
"t",
"pi",
"1",
"440*t"
],
"nodeFunctions": [
"+",
"-",
"round",
"sin",
"^",
"abs",
"ceil",
"cos"
]
},
{
"equation": "(log((log(220*t) / round(440*t))) + log((log(220*t) / round(440*t))))",
"fullEquation": "sin(2 * pi * ((log((log(220*t) / round(440*t))) + log((log(220*t) / round(440*t))))))",
"friendlyName": "PzingIngIngIng",
"id": "9B5-3:77:1",
"timestamp": "2025-11-01T22:47:14.206Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"(log(220*t) / round(440*t))"
],
"nodeFunctions": [
"+",
"log"
]
},
{
"equation": "(log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t))))",
"fullEquation": "sin(2 * pi * ((log((log(220*t) / round(440*t))) - sin((log(220*t) / round(440*t))))))",
"friendlyName": "PingIngIngIng",
"id": "9B5-3:77:1",
"timestamp": "2025-11-01T22:46:39.567Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"(log(220*t) / round(440*t))"
],
"nodeFunctions": [
"-",
"log",
"sin"
]
},
{
"equation": "(log(220*t) / round(440*t))",
"fullEquation": "sin(2 * pi * ((log(220*t) / round(440*t))))",
"friendlyName": "ShortStrum",
"id": "8B5-3:77:1",
"timestamp": "2025-11-01T22:44:58.461Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"220*t",
"440*t"
],
"nodeFunctions": [
"/",
"log",
"round"
]
},
{
"equation": "cos(log(cos(ceil(((abs(round(0.5)) * (t / cos(440*t))) ^ ((pi - pi) + cos(pi)))))))",
"fullEquation": "sin(2 * pi * (cos(log(cos(ceil(((abs(round(0.5)) * (t / cos(440*t))) ^ ((pi - pi) + cos(pi)))))))))",
"friendlyName": "3ProgressiveHums",
"id": "DB5-7:77:1",
"timestamp": "2025-11-01T22:36:57.962Z",
"depth": 8,
"width": 3,
"leaves": 4,
"nodes": 12,
"leafValues": [
"(abs(round(0.5)) * (t / cos(440*t)))",
"pi"
],
"nodeFunctions": [
"cos",
"log",
"ceil",
"^",
"+",
"-"
]
},
{
"equation": "cos(log(sin(ceil(((abs(round(0.5)) * (t / cos(440*t))) ^ ((pi - pi) + cos(pi)))))))",
"fullEquation": "sin(2 * pi * (cos(log(sin(ceil(((abs(round(0.5)) * (t / cos(440*t))) ^ ((pi - pi) + cos(pi)))))))))",
"friendlyName": "",
"id": "DB5-7:77:1",
"timestamp": "2025-11-01T22:36:12.657Z",
"depth": 8,
"width": 3,
"leaves": 4,
"nodes": 12,
"leafValues": [
"(abs(round(0.5)) * (t / cos(440*t)))",
"pi"
],
"nodeFunctions": [
"cos",
"log",
"sin",
"ceil",
"^",
"+",
"-"
]
},
{
"equation": "sin(sqrt(sign(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))",
"fullEquation": "sin(2 * pi * (sin(sqrt(sign(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))))",
"friendlyName": "FasterPhasers2",
"id": "DB5-7:77:1",
"timestamp": "2025-11-01T22:35:16.859Z",
"depth": 8,
"width": 3,
"leaves": 4,
"nodes": 12,
"leafValues": [
"220*t",
"sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))",
"cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))"
],
"nodeFunctions": [
"sin",
"sqrt",
"sign",
"ceil",
"/",
"+",
"cos"
]
},
{
"equation": "sin(sqrt(log(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))",
"fullEquation": "sin(2 * pi * (sin(sqrt(log(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))))",
"friendlyName": "FasterPhasers",
"id": "DB5-7:77:1",
"timestamp": "2025-11-01T22:34:57.062Z",
"depth": 8,
"width": 3,
"leaves": 4,
"nodes": 12,
"leafValues": [
"220*t",
"sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))",
"cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))"
],
"nodeFunctions": [
"sin",
"sqrt",
"log",
"ceil",
"/",
"+",
"cos"
]
},
{
"equation": "sin(sqrt(tan(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))",
"fullEquation": "sin(2 * pi * (sin(sqrt(tan(ceil((220*t / ((sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi))))) + sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) / cos(cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t))))))))))))))",
"friendlyName": "MixedStatic",
"id": "DB5-7:77:1",
"timestamp": "2025-11-01T22:34:39.721Z",
"depth": 8,
"width": 3,
"leaves": 4,
"nodes": 12,
"leafValues": [
"220*t",
"sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))",
"cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))"
],
"nodeFunctions": [
"sin",
"sqrt",
"tan",
"ceil",
"/",
"+",
"cos"
]
},
{
"equation": "(sqrt(sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) * sin(E))",
"fullEquation": "sin(2 * pi * ((sqrt(sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))) * sin(E))))",
"friendlyName": "BwawaawaaWaWaWa",
"id": "CB5-3:77:1",
"timestamp": "2025-11-01T22:33:08.276Z",
"depth": 3,
"width": 2,
"leaves": 2,
"nodes": 5,
"leafValues": [
"sin(sqrt(((abs(round(0.5)) * (t / cos(440*t))) + ((1 * (abs(round(0.5)) * (t / cos(440*t)))) * (220*t ^ pi)))))",
"E"
],
"nodeFunctions": [
"*",
"sqrt",
"sin"
]
},
{
"equation": "cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))",
"fullEquation": "sin(2 * pi * (cos(tan((0.5 + ((440*t - (abs(round(0.5)) * (t / cos(440*t)))) * (pi / 220*t)))))))",
"friendlyName": "",
"id": "AB5-5:77:1",
"timestamp": "2025-11-01T22:32:37.102Z"
},
{
"equation": "(ceil(t) / sqrt((abs(round(0.5)) * (t / cos(440*t)))))",
"fullEquation": "sin(2 * pi * ((ceil(t) / sqrt((abs(round(0.5)) * (t / cos(440*t)))))))",
"friendlyName": "DwummmUmmm",
"id": "9B5-3:77:1",
"timestamp": "2025-11-01T22:17:37.045Z"
},
{
"equation": "(abs(round(0.5)) * (t / cos(440*t)))",
"fullEquation": "sin(2 * pi * ((abs(round(0.5)) * (t / cos(440*t)))))",
"friendlyName": "(abs(round0.5)*(t/cos440*t))",
"id": "8B5-3:237:1",
"timestamp": "2025-11-01T21:45:40.820Z"
}
]